已知函数y=kx+b的图象经过点A(- 3, - 2)及点B(1, 6).
(1)求此一次函数解析式,并画图象; (2)求函数y=2x+4图象与坐标轴围成的三角形的面积.
计算:
(1)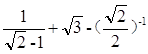
(2)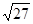 +(
+(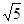 -1)0+
-1)0+
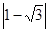
在矩形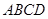 中,
中,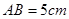 ,
,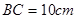 ,点
,点 从点
从点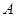 沿矩形的边以
沿矩形的边以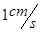 的速度经
的速度经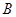 向
向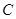 运动,点
运动,点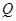 从
从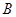 点出发沿矩形的边以
点出发沿矩形的边以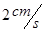 的速度经
的速度经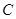 向
向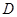 运动,点
运动,点 、
、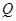 同时运动,且一点到达终点另一点也停止运动,求几秒后以
同时运动,且一点到达终点另一点也停止运动,求几秒后以 、
、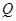 、
、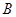 为顶点的三角形的面积等于6平方厘米?
为顶点的三角形的面积等于6平方厘米?
先化简,再求值: ,其中x满足方程:x2+x﹣6=0。
,其中x满足方程:x2+x﹣6=0。
如图,正方形ABCD的边长为3,E,F 分别是AB,BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM. 
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.