请阅读下列材料:
问题:如图1,点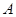 ,
, 在直线
在直线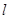 的同侧,在直线
的同侧,在直线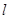 上找一点
上找一点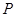 ,使得
,使得 的值最小.小明的思路是:如图2,作点
的值最小.小明的思路是:如图2,作点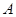 关于直线
关于直线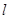 的对称点
的对称点 ,连接
,连接 ,则
,则 与直线
与直线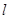 的交点
的交点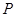 即为所求.
即为所求.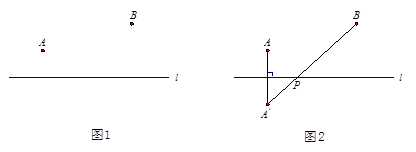
请你参考小明同学的思路,探究并解决下列问题:
(1)如图3,在图2的基础上,设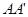 与直线
与直线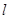 的交点为
的交点为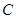 ,过点
,过点 作
作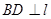 ,垂足为
,垂足为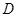 .若
.若 ,
, ,
,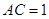 ,写出
,写出 的值为 ;
的值为 ;
(2)将(1)中的条件“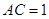 ”去掉,换成“
”去掉,换成“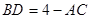 ”,其它条件不变,写出此时
”,其它条件不变,写出此时 的值 ;
的值 ;
(3) +
+ 的最小值为 .
的最小值为 .
如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37º,求∠D的度数
解不等式:5x–12≤2(4x-3)
已知抛物线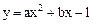 经过点A(
经过点A(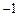 ,0)、B(m,0)(m>0),且与y轴交于点C.
,0)、B(m,0)(m>0),且与y轴交于点C.
⑴求a、b的值(用含m的式子表示)
⑵如图所示,⊙M过A、B、C三点,求阴影部分扇形的面积S(用含m的式子表示);
⑶在x轴上方,若抛物线上存在点P,
使得以A、B、P为顶点的三角形与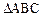 相似,求m的值.
相似,求m的值.
已知△ABC ,D、E、F分别是AB、AC、BC上的点。且DE∥BC, EF∥AB.
求证:
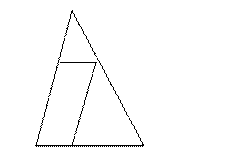
已知如图,AB和DE是直立在地面上的两根立柱,AB=10m,某一时刻AB在太阳光下的投影BC=6m.21世纪教育网
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为3m,计算DE的长.