如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．
（1）如图②，已知Rt△ABC中，∠ACB=90°，∠ACB＞∠A，CD是AB上的中线，过点B作BE⊥CD，垂足为E，试说明E是△ABC的自相似点．
（2）如图③，在△ABC中，∠A＜∠B＜∠C．
①利用尺规作出△ABC的自相似点P（不写出作法，保留作图痕迹）；
②如果△ABC的内心P是该三角形的自相似点，请直接写出该三角形三个内角的度数．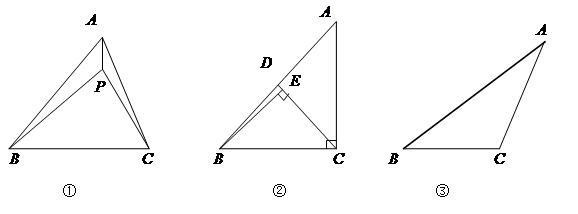
已知关于x、y的方程组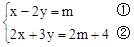
的解满足不等式组
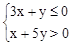。求满足条件的m的整数值。
如图，AB是⊙O的直径，经过圆上点D的直线CD恰∠ADC=∠B。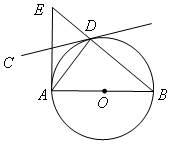
（1）求证：直线CD是⊙O的的切线；
（2）过点A作直线AB的垂线交BD的延长线于点E，且AB=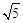
，BD=2，求线段AE的长。
如图，山顶有一铁塔AB的高度为20米，为测量山的高度BC，在山脚D处测得塔顶A和塔基B的仰角分别为600和450。求山的高度BC（结果保留根号）。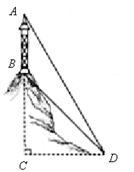
中学生带手机上学的现象越来越受到社会的关注，为此，某记者随机调查了某城区若干名学生家长对这种现象的态度（态度分为：A：无所谓；B：基本赞成；C：赞成；D：反对），并将调查结果绘制成频数折线图1和统计图2（不完整）。请根据图中提供的信息，解答下列问题：
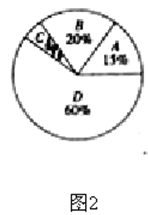
（1）此次抽样检查中，共调查了 名学生家长；
（2）将图1补充完整；
（3）根据抽样检查的结果，请你估计该市城区6000名中学生家长中有多少名家长持反对态度？
化简并求值：
，其中x、y满足