已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.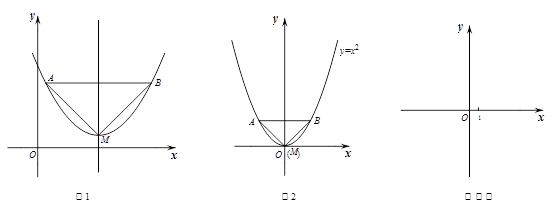
(1)①如图2,求出抛物线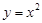 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线 与
与 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线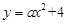 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线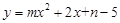 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且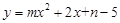 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
如图所示,在平面直角坐标系中,顶点为(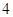 ,
,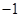 )的抛物线交
)的抛物线交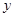 轴于
轴于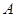 点,交
点,交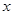 轴于
轴于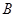 ,
,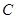 两点(点
两点(点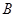 在点
在点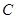 的左侧), 已知
的左侧), 已知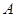 点坐标为(
点坐标为( ,
,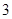 ).
).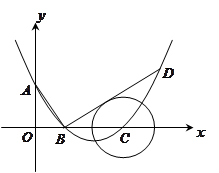
(1)求此抛物线的解析式;
(2)过点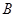 作线段
作线段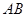 的垂线交抛物线于点
的垂线交抛物线于点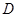 ,
,
如果以点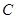 为圆心的圆与直线
为圆心的圆与直线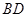 相切,请判断抛物
相切,请判断抛物
线的对称轴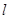 与⊙
与⊙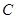 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点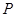 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于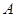 ,
,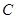 两点之间,问:当点
两点之间,问:当点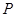 运动到什么位置时,
运动到什么位置时,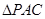 的
的
面积最大?并求出此时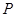 点的坐标和
点的坐标和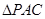 的最大面积.
的最大面积.
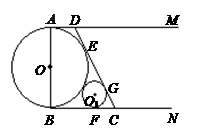
如图所示,⊙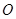 的直径
的直径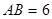 ,
,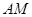 和
和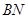 是它的两条切线,
是它的两条切线,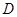 为射线
为射线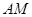 上的动点(不与
上的动点(不与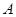 重合),
重合),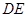 切⊙
切⊙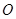 于
于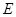 ,交
,交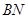 于
于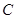 ,设
,设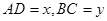 .
.
(1)求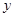 与
与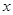 的函数关系式;
的函数关系式;
(2)若⊙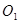 与⊙
与⊙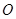 外切,且⊙
外切,且⊙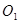 分别与
分别与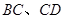
相切于点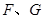 ,求
,求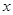 为何值时⊙
为何值时⊙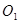 半径为1.
半径为1.
“知识改变命运,科技繁荣祖国”.我市中小学每年都要举办一届科技比赛.下图为
我市某校2011年参加科技比赛(包括电子百拼、航模、机器人、建模四个类别)的参赛人数统计图: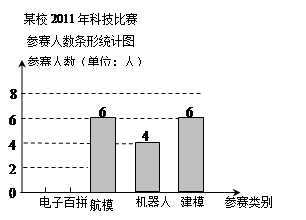
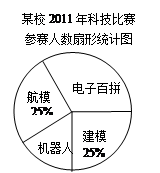
(1)该校参加机器人、建模比赛的人数分别是人和人;
(2)该校参加科技比赛的总人数是人,电子百拼所在扇形的圆心角的度数是°,并把条形统计图补充完整;
(3)从全市中小学参加科技比赛选手中随机抽取80人,其中有32人获奖. 2011年我市中小学参加科技比赛人数共有2485人,请你估算2011年参加科技比赛的获奖人数约是多少人?
如图所示,AB//CD,∠ACD= .
.
⑴用直尺和圆规作∠C的平分线CE,交AB于E,并在CD
上取一点F,使AC=AF,再连接AF,交CE于K;
(要求保留作图痕迹,不必写出作法)
⑵依据现有条件,直接写出图中所有相似的三角形﹒
(图中不再增加字母和线段,不要求证明)
如图所示,一次函数 与反比例函数
与反比例函数 的图象相交于A,B两点,且与坐标轴的交点为
的图象相交于A,B两点,且与坐标轴的交点为 ,
, ,点B的横坐标为
,点B的横坐标为 .
.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式 的解.
的解.