若函数f(x) (x∈R)是奇函数,则
| A.函数f(x2)是奇函数 |
| B.函数[f(x)]2是奇函数 |
C.函数f(x)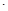 x2是奇函数 x2是奇函数 |
| D.函数f(x)+x2是奇函数 |
如图是函数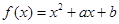 的部分图象,则函数
的部分图象,则函数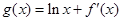 的零点所在的区间是()
的零点所在的区间是()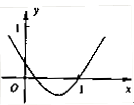
A.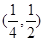 |
B.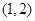 |
C. |
D.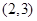 |
观察数列:3,2,6,5,15,14,x,y,z,122,……,其中x,y,z的值依次是()
| A.42,41,123 | B.13,39,123 |
| C.24,23,123 | D.28,27,123 |
如果函数 对于区间D内任意的
对于区间D内任意的 ,有
,有

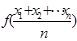 成立,称
成立,称 是区间D上的“凸函数”.已知函数
是区间D上的“凸函数”.已知函数 在区间
在区间 上是“凸函数”,则在△
上是“凸函数”,则在△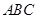 中,
中, 的最大值是()
的最大值是()
A.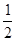 |
B. |
C.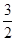 |
D. |
下面几种推理中是演绎推理的序号为()
| A.由金、银、铜、铁可导电,猜想:金属都可导电; |
B.猜想数列 的通项公式为 的通项公式为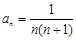 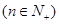 ; ; |
C.半径为 圆的面积 圆的面积 ,则单位圆的面积 ,则单位圆的面积 ; ; |
D.由平面直角坐标系中圆的方程为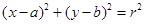 ,推测空间直角坐标系中球的方程为 ,推测空间直角坐标系中球的方程为 . . |
用反证法证明命题“三角形的内角中至少有一个不大于60度”时,反设正确的是()
| A.假设三内角都不大于60度 | B.假设三内角都大于60度 |
| C.假设三内角至多有一个大于60度 | D.假设三内角至多有两个大于60度 |