【问题引入】
几个人拎着水桶在一个水龙头前面排队打水,水桶有大有小.他们该怎样排队才能使得总的排队时间最短?
假设只有两个人时,设大桶接满水需要T分钟,小桶接满水需要t分钟(显然T>t),若拎着大桶者在拎小桶者之前,则拎大桶者可直接接水,只需等候T分钟,拎小桶者一共等候了(T+t)分钟,两人一共等候了(2T+t)分钟;反之,若拎小桶者在拎大桶者之前,容易求出两人接满水等候(T+2t)分钟。可见,要使总的排队时间最短。拎小桶者应排在拎大桶者前面。这样,我们可以猜测,几个人拎着水桶在一个水龙头前面排队打水,要使总的排队时间最短,需将他们按水桶从小到大排队.
规律总结:
事实上,只要不按照从小到大的顺序排队,就至少有紧挨着的两个人拎大桶者排在拎小桶者之前,仍设大桶接满水需要T分钟,小桶接满水需t分钟,并设拎大桶者开始接水时已经等候了m分钟,这样拎大桶者接满水一共等候了(m+T)分钟,拎小桶者接满水一共等候了(m+T+t)分钟,两人共等候了(2m+2T+t)分钟,在其他人位置不变的前提下,让这两个人交换位置,即局部调整这两个人的位置,同样可以计算两个人接满水共等候了 __ ___分钟,共节省了 _________分钟,而其他人的等候时间未变。这说明只要存在有紧挨着的两个人是拎大桶者在拎小桶者前,都可以这样局部调整,从而使得总等候时间减少。这样经过一系列调整之后,整个队伍都是从小到大排列,就达到最优状态,总的排队时间就最短.
【方法探究】
一般地,对某些涉及多个可变对象的数学问题,先对其少数对象进行调整,其他对象暂时保持不变,从而化难为易,取得问题的局部解决.经过若干次这种局部的调整,不断缩小范围,逐步逼近目标,最终使问题得到解决,这种数学思想方法就叫做局部调整法.
【实践应用1】
如图1,在锐角△ABC中,AB=4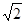 ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
解析:(1)先假定N为定点,调整M到合适位置,使BM+MN有最小值(相对的).
容易想到,在AC上作AN′=AN(即作点N关于AD的对称点N′),连接BN′交AD于M,则M点是使BM+MN有相对最小值的点.(如图2,M点确定方法找到)
(2)再考虑点N的位置,使BM+MN最终达到最小值.
可以理解,BM+MN = BM+MN′,所以要使BM+MN′有最小值,只需使 ,此时BM+MN的最小值为 .
【实践应用2】
如图,把边长是3的正方形等分成9个小正方形,在有阴影的两个小正方形内(包括边界)分别任取点P、R,与已知格点Q(每个小正方形的顶点叫做格点)构成三角形,求△PQR的最大面积,并在图2中画出面积最大时的△PQR的图形.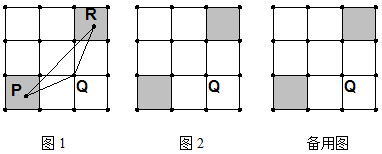
化简或化简求值(每小题6分,共12分)
(1)|a-2|+(b+3)2=0,求3a2b-[2ab2-2(ab-1.5a2b)+ab]+3ab2的值;
(2)已知有理数a、b、c在数轴上的对应点如图所示,化简:|b-a|+|a+c|-2|c-b|.
某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案1:从包装盒加工厂直接购买,购买所需的费用y1与包装盒数x满足如图的函数关系。
方案2:租赁机器自己加工,所需费用y2(包括租赁机器的费用和生产包装盒的费用)与包装盒数x满足如图的函数关系。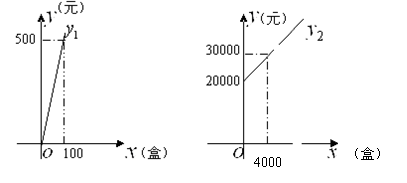
根据图象回答下列问题:
(1)方案1中每个包装盒的价格是多少元?
(2)方案2中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1,、y2与x的函数表达式;
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由。
|
阅读理解题: 如图,在△ABC中,AD是BC边上的中线,且AD=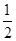 BC.
BC.
求证:∠BAC=90°.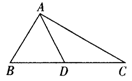
证明:∵AD=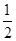 BC,BD=CD=
BC,BD=CD=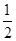 BC,
BC,
∴AD=BD=DC,
 ∴ADB和 ADC都是等腰三角形
∴ADB和 ADC都是等腰三角形
∴∠B=∠BAD,∠C=∠CAD,
∵∠B+∠BAD+∠CAD+∠C=180°,
∴∠BAD+∠CAD=90°,即∠BAC=90°.
(1)此题实际上是直角三角形的另一个判定方法,请你用文字语言叙述出来.
(2)直接运用这个结论解答题目:一个三角形一边长为2,这边上的中线长为1,另两边之和为1+ ,求这个三角形的面积.
,求这个三角形的面积.
【知识储备:勾股定理:在直角三角形中。两直角边的平方和等于斜边的平方。】
某校运动会需购买A、B两种奖品.若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍.设购买A种奖品m件,购买费用为W元,求出W(元)与m(件)之间的函数关系式,求出自变量m的取值范围,并确定最少费用W的值.
如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.
(1)填空:A,B两地相距千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?