如图，已知正比例函数y = ax（a≠0）的图象与反比例函致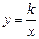
（k≠0）的图象的一个交点为A（－1，2－k2），另—个交点为B，且A、B关于原点O对称，D为OB的中点，过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E．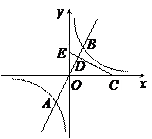
（1）写出反比例函数和正比例函数的解析式；
（2）试计算△COE的面积是△ODE面积的多少倍．
绵阳农科所为了考察某种水稻穗长的分布情况，在一块试验田里随机抽取了50个谷穗作为样本，量得它们的长度（单位：cm）．对样本数据适当分组后，列出了如下频数分布表：
| 穗长 |
4.5≤x＜5 |
5≤x＜5.5 |
5.5≤x＜6 |
6≤x＜6.5 |
6.5≤x＜7 |
7≤x＜7.5 |
| 频数 |
4 |
8 |
12 |
13 |
10 |
3 |
（1）在图1、图2中分别出频数分布直方图和频数折线图；
（2）请你对这块试验田里的水稻穗长进行分析；并计算出这块试验田里穗长在5.5≤x＜7范围内的谷穗所占的百分比．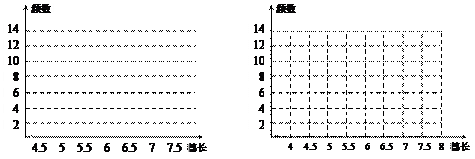
图1图2
已知关于x的一元二次方程x2 = 2（1－m）x－m2 的两实数根为x1，x2．
（1）求m的取值范围；
（2）设y = x1 + x2，当y取得最小值时，求相应m的值，并求出最小值．
如图，抛物线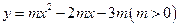
与
轴交于
两点，与
轴交于
点.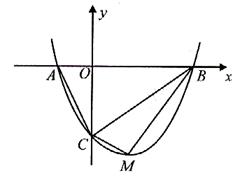
（1）请求出抛物线顶点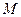
的坐标（用含
的代数式表示），两点的坐标；
（2）经探究可知，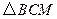
与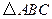
的面积比不变，试求出这个比值；
（3）是否存在使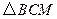为直角三角形的抛物线？若存在，请求出；如果不存在，请说明
理由.
如图，在
中，
点
在斜边
上，以
为直径的
与
相切于点
（1）求证：
平分
（2）若
①求的值；②求图中阴影部分的面积.
．