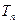(本小题满分12分).已知向量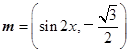 ,
,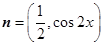 ,函数
,函数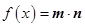 .
.
(Ⅰ)试用五点作图法画出函数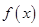 在一个周期内的图象(要求列表);
在一个周期内的图象(要求列表);
(Ⅱ)求方程 在
在 内的所有实数根之和.
内的所有实数根之和.
(本小题满分14分)
已知等差数列{an}的前n项和为Sn,a1=1+,S3=9+3
(1)求数列{an}的通项an与前n项和Sn;
(2)设 ,求证:数列{bn}中任意不同的三项都不可能成为等比数列.
,求证:数列{bn}中任意不同的三项都不可能成为等比数列.
(本小题满分14分)
已知集合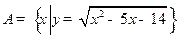 ,集合
,集合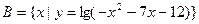 ,集合
,集合 .
.
(1)求 ;
;
(2)若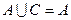 ,求实数
,求实数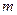 的取值范围.
的取值范围.
设函数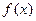 是定义域在
是定义域在 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数 有
有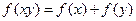 ,已知
,已知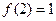 .
.
(1)求 的值;
的值;
(2)一个各项均为正数的数列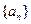 满足:
满足: ,其中
,其中 是数列
是数列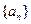 的前n项的和,求数列
的前n项的和,求数列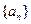 的通项公式;
的通项公式;
(3)在(2)的条件下,是否存在正数 ,
,
使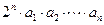

已知函数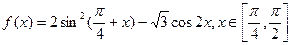 。
。
(1)求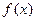 的最大值与最小值。
的最大值与最小值。
(2)若不等式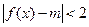 在
在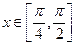 恒成立,求实数
恒成立,求实数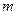 的取值范围
的取值范围
20.等比数列{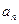 }的前n项和为
}的前n项和为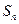 , 已知对任意的
, 已知对任意的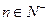 ,点
,点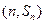 均在函数
均在函数 且
且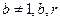 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(2)当b=2时,记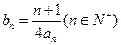 求数列
求数列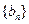 的前
的前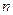 项和
项和