(本小题满分14分)
已知等差数列{an}的前n项和为Sn,a1=1+,S3=9+3
(1)求数列{an}的通项an与前n项和Sn;
(2)设 ,求证:数列{bn}中任意不同的三项都不可能成为等比数列.
,求证:数列{bn}中任意不同的三项都不可能成为等比数列.
已知圆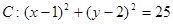 ,直线
,直线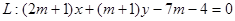
(1)求证:直线恒过定点
(2)判断直线被圆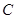 截得的弦长何时最短?并求截得的弦长最短时
截得的弦长何时最短?并求截得的弦长最短时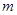 的值及最短长度。
的值及最短长度。
已知集合A= ,B=
,B=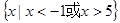 .
.
(1) 若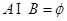 ,求实数
,求实数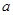 的取值范围;
的取值范围;
(2) 若 ,求实数
,求实数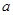 的取值范围.
的取值范围.
定义在 上的奇函数
上的奇函数 ,当
,当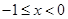 时,
时,
(1)求 在
在 上的解析式;
上的解析式;
(2)判断 在
在 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当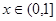 时,关于
时,关于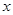 的方程
的方程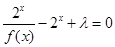 有解,试求实数
有解,试求实数 的取值范围.
的取值范围.
(本小题满分12)
为了绿化城市,准备在如图所示的区域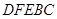 内修建一个矩形
内修建一个矩形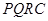 的草坪,并建立如图平面直角坐标系,且
的草坪,并建立如图平面直角坐标系,且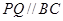 ,
,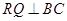 ,另外
,另外 的内部有一文物保护区不能占用,经测量
的内部有一文物保护区不能占用,经测量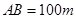 ,
,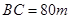 ,
, 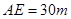 ,
,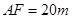 .
.
(1)求直线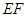 的方程;
的方程;
(2)应如何设计才能使草坪的占地面积最大?并求最大面积。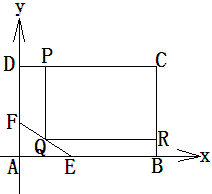
写出下列命题的否定.
(1) 对所有的正数x, 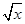 >x-1
>x-1
(2) 不存在实数x,x2+1<2x”
(3) 集合A中的任意一个元素都是集合B的元素
(4) 集合A中至少有一个元素是集合B的元素