(本小题满分12)
为了绿化城市,准备在如图所示的区域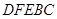 内修建一个矩形
内修建一个矩形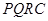 的草坪,并建立如图平面直角坐标系,且
的草坪,并建立如图平面直角坐标系,且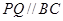 ,
,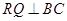 ,另外
,另外 的内部有一文物保护区不能占用,经测量
的内部有一文物保护区不能占用,经测量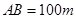 ,
,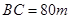 ,
, 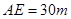 ,
,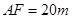 .
.
(1)求直线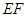 的方程;
的方程;
(2)应如何设计才能使草坪的占地面积最大?并求最大面积。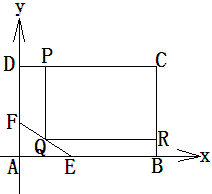
设函数

(1)若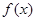 的最小值为3,求
的最小值为3,求 的值;
的值;
(2)求不等式 的解集.
的解集.
已知曲线 (
( 为参数),
为参数), (
( 为参数).
为参数).
(1)化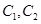 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)过曲线 的左顶点且倾斜角为
的左顶点且倾斜角为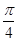 的直线
的直线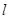 交曲线
交曲线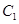 于
于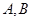 两点,求
两点,求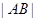 .
.
如图, 四点在同一圆上,
四点在同一圆上,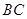 与
与 的延长线交于点
的延长线交于点 ,点
,点 在
在 的延长线上.
的延长线上.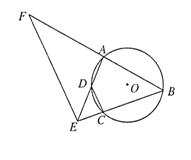
(1)若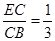 ,
,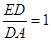 ,求
,求 的值;
的值;
(2)若 ,证明:
,证明: .
.
(本小题满分12分)已知函数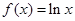 ,
,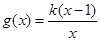 .
.
(1)当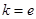 时,求函数
时,求函数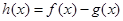 的单调区间和极值;
的单调区间和极值;
(2)若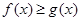 恒成立,求实数
恒成立,求实数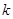 的值.
的值.
(本小题满分12分)已知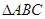 的两顶点坐标
的两顶点坐标 ,
,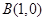 ,圆
,圆 是
是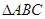 的内切圆,在边
的内切圆,在边 ,
, ,
,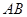 上的切点分别为
上的切点分别为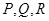 ,
, (从圆外一点到圆的两条切线段长相等),动点
(从圆外一点到圆的两条切线段长相等),动点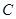 的轨迹为曲线
的轨迹为曲线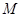 .
.
(1)求曲线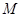 的方程;
的方程;
(2)设直线 与曲线
与曲线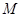 的另一交点为
的另一交点为 ,当点
,当点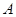 在以线段
在以线段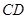 为直径的圆上时,求直线
为直径的圆上时,求直线 的方程.
的方程.