(本小题满分12分)已知函数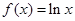 ,
,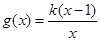 .
.
(1)当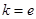 时,求函数
时,求函数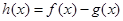 的单调区间和极值;
的单调区间和极值;
(2)若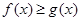 恒成立,求实数
恒成立,求实数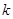 的值.
的值.
(本小题满分13分)
已知椭圆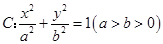 的一个焦点和抛物线
的一个焦点和抛物线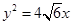 的焦点相同,过椭圆右焦点F且垂直
的焦点相同,过椭圆右焦点F且垂直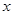 轴的弦长为2.
轴的弦长为2.
(I)求椭圆C的方程;
(II)若与直线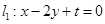 相垂直的直线
相垂直的直线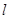 与椭圆C交于B、D两点,求
与椭圆C交于B、D两点,求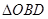 的最大值.
的最大值.
(本小题满分12分)
如图,四边形ACDF为正方形,平面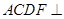 平面BCDE,平面
平面BCDE,平面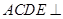 平面ABC,BC=2DE,DE//BC, M为AB的中点.
平面ABC,BC=2DE,DE//BC, M为AB的中点.
(I)证明: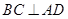 ;
;
(II)证明:EM//平面ACDF.
(本小题满分12分)
各项均为正数的数列 的前
的前 项和为
项和为 ,已知点
,已知点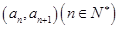 在函数
在函数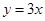 的图象上,且
的图象上,且
(I)求数列 的通项公式;
的通项公式;
(II)在 之间插入
之间插入 个数,使这
个数,使这 个数组成公差为
个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)
已知函数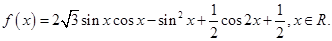
(I)求函数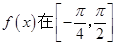 上的最值;
上的最值;
(II)若将函数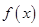 的图象向右平移
的图象向右平移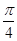 个单位,再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到
个单位,再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到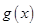 的图象.已知
的图象.已知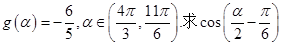 的值.
的值.
(本小题满分12分)
某中学举行了一次“社会主义核心价值观知识竞赛”活动,为了解本次竞赛中学生成绩情况,从全体学生中随机抽取了部分学生的分数(得分取整数且不低于50分,满分100分),作为样本(样本容量为n)进行统计.按照
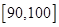 的分组作出频率分布直方图,并作出茎叶图(图中仅列出来
的分组作出频率分布直方图,并作出茎叶图(图中仅列出来 这两组的数据).
这两组的数据).
(I)求样本容量n和频率分布直方图中的 ;
;
(II)在选取的样本中,从样本中竞赛成绩80分以上(含80分)的同学中随机抽取2名同学到市政广场参加社会主义核心价值观知识宣传志愿者活动.求所抽取的2名同学来自不同组的概率.