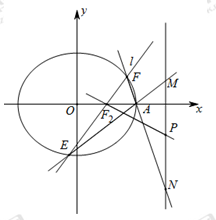
已知圆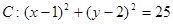 ,直线
,直线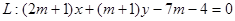
(1)求证:直线恒过定点
(2)判断直线被圆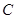 截得的弦长何时最短?并求截得的弦长最短时
截得的弦长何时最短?并求截得的弦长最短时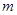 的值及最短长度。
的值及最短长度。
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为 ,求
,求 ;
;
(2)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
在如图所示的几何体中, 平面
平面 ,
, ∥
∥ ,
, 是
是 的中点,
的中点, ,
, .
.
(1)证明: ∥平面
∥平面 ;
;
(2)求二面角 的大小的余弦值.
的大小的余弦值.
已知函数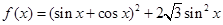 .
.
(1)求函数f (x)的最小正周期;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足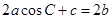 ,求f(B)的取值范围.
,求f(B)的取值范围.
已知数列 的各项均为正数,记
的各项均为正数,记 ,
, ,
,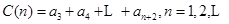 .
.
(1)若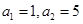 ,且对任意
,且对任意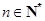 ,三个数
,三个数 组成等差数列,求数列
组成等差数列,求数列 的通项公式.
的通项公式.
(2)证明:数列 是公比为
是公比为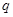 的等比数列的充分必要条件是:对任意
的等比数列的充分必要条件是:对任意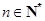 ,三个数
,三个数 组成公比为
组成公比为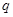 的等比数列.
的等比数列.
已知椭圆 的左右焦点分别为
的左右焦点分别为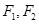 ,点
,点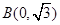 为短轴的一个端点,
为短轴的一个端点,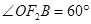 .
.
(1)求椭圆 的方程;
的方程;
(2)如图,过右焦点 ,且斜率为
,且斜率为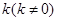 的直线
的直线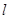 与椭圆
与椭圆 相交于
相交于 两点,
两点, 为椭圆的右顶点,直线
为椭圆的右顶点,直线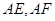 分别交直线
分别交直线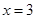 于点
于点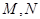 ,线段
,线段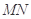 的中点为
的中点为 ,记直线
,记直线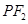 的斜率为
的斜率为 .
.
求证: 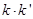 为定值.
为定值.