(1)如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BF=AE.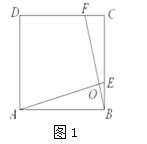
(2) 如图2,正方形ABCD边长为12,将正方形沿MN折叠,使点A落在DC边上的点E处,且DE=5,求折痕MN的长.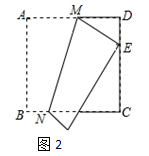
(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4.直接写出下列两题的答案:①如图3,矩形ABCD由2个全等的正方形组成,则 GH=___________;
②如图4,矩形ABCD由n个全等的正方形组成,则 GH=___________;(用n的代数式表示).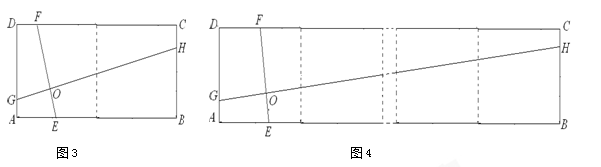
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个面积为5的等腰直角三角形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、 、
、  ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
已知:A(0,1),B(2,0),C(4,3)
(1)在坐标系中描出各点,画出△ABC.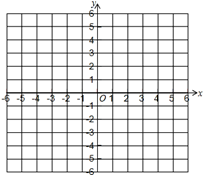
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
解下列不等式组,并将解集在数轴上表示出来。
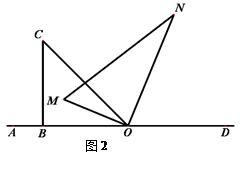
将一副直角三角板如图1摆放在直线AD上(直角三角板OBC和直角三角板MON ,∠OBC=90°,∠BOC=45°,∠MON = 90°,∠MNO = 30°),保持三角板OBC不动,将三角板MON绕点O以每秒10°的速度顺时针旋转,旋转时间为t秒
(1)当t= 秒时, OM平分∠AOC?如图2,此时∠NOC-∠AOM= °;
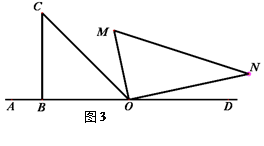
(2)继续旋转三角板MON,如图3,使得OM、ON同时在直线OC的右侧,猜想∠NOC与∠AOM有怎样的数量关系?并说明理由;
(3)若在三角板MON开始旋转的同时,另一个三角板OBC也绕点O以每秒5°的速度顺时针旋转,当OM旋转至射线OD上时同时停止,(自行画图分析)
①当t= 秒时,OM平分∠AOC?
②请直接写出在旋转过程中,∠NOC与∠AOM的数量关系.