随着大陆惠及台胞政策措施的落实，台湾水果进入了大陆市场．一水果经销商购进了A、B两种台湾水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售，预计每箱水果的盈利情况如下表：
有两种配货方式（整箱配货）
方案一：甲乙两店各配货10箱，其中A种水果两店各5箱，B种水果两店各5箱；
方案二：按照甲乙两店盈利相同配货，其中A种水果甲店 箱，乙店 箱，B种水果甲店 箱，乙店 箱
（1）如果按照方案一配货，请你计算出经销商能盈利多少元；
（2）请你将方案二填写完整（只写一种情况即可），并根据你填写的方案二与方案一作比较，哪种方案盈利较多．（本题6分）
某农场
名职工耕种
公顷土地，分别种植水稻、蔬菜和棉花，种植这些农作物每公顷所需人数如表1；另外设水稻和蔬菜的种植面积分别为
公顷、
公顷，每公顷各种农作物预计产值如表2。
用含
的式子表示。为完成国家的粮食任务，水稻、蔬菜和棉花的种植面积至少需要12公顷，且水稻、蔬菜和棉花的种植面积均为整数，那么水稻、蔬菜和棉花的种植面积应各为多少公顷？请安排出种植方案。
若设总产值为
，那么怎样安排种植面积才能取得最大效益？
在平原上有一条笔直的公路，在公路同侧有A、B两个村庄。若以公路为
轴建立平面直角坐标系，如图1：已知A、B两个村庄的坐标分别为（2，2），（7，4），一辆汽车（看成点P）在轴上行驶．汽车行驶过程中到A、B两村距离之和最小为多少？
汽车行驶过程中到A、B两村距离之差最大为多少？
宽与长的比是
的矩形叫黄金矩形．心理测试表明：黄金矩形令人赏心悦目，它给我们以协调，匀称的美感．现将小明同学在数学活动课中，折叠黄金矩形的方法归纳如下（如图所示）：
第一步：作一个正方形
；
第二步：分别取
，
的中点
，
，连接
；
第三步：以为圆心，
长为半径画弧，交的延长线于
；
第四步：过作
⊥，交的延长线于
。
请你根据以上作法，证明矩形
为黄金矩形。
△ABC的三边满足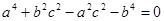
，请判别△ABC的形状。
已知一次函数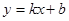
中，当
时，函数值为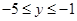
。求：这个一次函数的解析式？并画出这个一次函数的图像。
求出这个函数图象与另一个正比例函数
的交点坐标，并根据图象写出使一次函数的值大于正比例函数的值时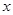
的取值范围。