在平面内，将一个图形
以任意点
为旋转中心，逆时针旋转一个角度
，得到图形
，再以为中心将图形
放大或缩小得到图形 ，使图形
与图形
对应线段的比为
，并且图形上的任一点
，它的对应点
在线段
或其延长线上；我们把这种图形变换叫做旋转相似变换，记为
，其中点叫做旋转相似中心，叫做旋转角，
叫做相似比．如图1中的线段
便是由线段
经过
得到的．
（1）如图2，将△ABC经过☆
后得到△
，则横线上“☆”应填下列
四个点
、
、
、
中的点 ．
（2）如图3，△ADE是△ABC经过
得到的，
，
则这个图形变换可以表示为
（ ， ）．
计算：（1）2-3－22×0.25＋20130 (2) 
如图，(1)P是等腰三角形A BC底边BC上的一人动点，过点P作BC的垂线，交AB于点Q，交CA的延长线于点R。请观察AR与AQ，它们有何关系？并证明你的猜想。
(2)如果点P沿着底边BC所在的直线，按由C向B的方向运动到CB的延长线上时，(1)中所得的结论还成立吗？请你在图15(2)中完成图 形，并给予证明。
如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.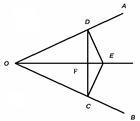
（1）求证：OE是CD的垂直平分线.
（2）若∠AOB=60º，请你探究OE，EF之间有什么数量关系？并证明你的结论。
如图，在四边形ABCD中BC=CD，点E是BC的中点，点F是CD的中点，且AE⊥BC，AF⊥CD。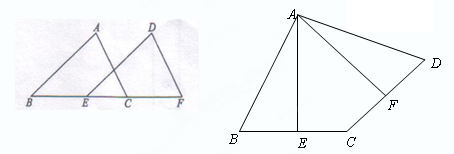
（1）求证：AB=AD。
（2）请你探究∠EAF，∠BAE，∠DAF之间有什么数量关系？并证明你的结论。
已知：点 B、E、C、F在同一直线上，AB＝DE，∠A＝∠D，AC∥DF．
求证：⑴ △ABC≌△DEF；
⑵ BE＝CF．