阅读下面材料：小强遇到这样一个问题：试作一个直角△ABC，使∠C=90°，AB=7，AC+BC=9．小强是这样思考的：如图1，假定直角△ABC已作出，延长AC到点D，使CD=CB，则AD=9，∠D=45°，因此可先作出一个辅助△ABD，再作BD的垂直平分线分别交AD于点C，BD于点E，连接BC，所得的△ABC即为所作三角形．具体做法小强是利用图2中1×1正方形网格，通过尺规作图完成的．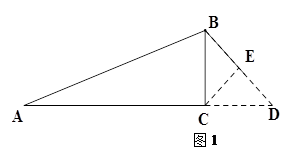
（1）请回答：图2中线段AB等于线段 ．
（2）参考小强的方法，解决问题：请在图3的菱形网格中（菱形最小内角为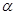
，边长为a），画出一个△ABC，使∠C=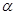，AB=6b，AC+BC=8b．（在图中标明字母，不写作法，保留作图痕迹）．
因式分解：
在数学活动中，小明为了求 
的值（结果用n表示），设计如图1所示的几何图形．请你利用这个几何图形求
的值为 ；请你利用图2，再设计一个能求
的值的几何图形．
A、B两地相距80千米，甲骑车从A地出发1小时后，乙也从A地出发，以甲的速度的1.5倍追赶，当乙到达B地时，甲已先到20分钟，求甲、乙的速度．
学校用一笔钱买奖品，若以1支钢笔和2本日记本为一份奖品，则可买60份奖品；若以1支钢笔和3本日记本为一份奖品，则可买50份奖品，问这笔钱全部用来买钢笔或日记本，可买多少？
有一道题“先化简，再求值： 
其中，x=-3”小玲做题时把“x=-3”错抄成了“x=
3”，但她的计算结果也是正确的，请你解释这是怎么回事？