(本小题满分15分)已知椭圆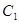 、抛物线
、抛物线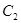 的焦点均在
的焦点均在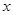 轴上,
轴上,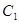 的中心和
的中心和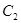 的顶点均为原点
的顶点均为原点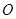 ,从每条曲线上取两个点,
,从每条曲线上取两个点,
将其坐标记录于下表中:
| x |
3 |
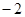 |
4 |
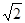 |
 |
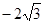 |
0 |
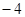 |
 |
(Ⅰ)求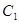 ,
,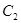 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线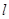 满足条件:①过
满足条件:①过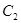 的焦点
的焦点 ;②与
;②与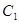 交于不同两点
交于不同两点 ,
, ,且满足
,且满足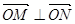 ?
?
若存在,求出直线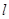 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知集合A={x|x2-4mx+2m+6=0},B={x|x<0},若命题“A∩B=∅”是假命题,求实数m的取值范围.
已知集合A= ,B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,求实数m的取值范围.
,B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,求实数m的取值范围.
已知集合A= ,B={x|m+1≤x≤2m-1}.
,B={x|m+1≤x≤2m-1}.
(1)求集合A;
(2)若B⊆A,求实数m的取值范围.
设集合A={x|x2+2x-3>0},B={x|x2-2ax-1≤0,a>0}.若A∩B中恰含有一个整数,求实数a的取值范围.
某电视台的一个智力游戏节目中,有一道将中国四大名著《三国演义》、《水浒传》、《西游记》、《红楼梦》与它们的作者连线的题目,每本名著只能与一名作者连线,每名作者也只能与一本名著连线,每连对一个得2分,连错得-1分,某观众只知道《三国演义》的作者是罗贯中,其他不知道随意连线,将他的得分记作ξ.
(1)求该观众得分ξ为负数的概率;
(2)求ξ的分布列.