(本小题满分12分)直三棱柱 中,
中,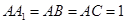 ,E,F分别是
,E,F分别是 的中点,
的中点,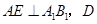 为棱
为棱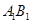 上的点.
上的点.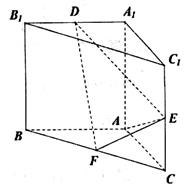
(Ⅰ)证明: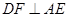 ;
;
(Ⅱ)已知存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为 ,请说明点D的位置.
,请说明点D的位置.
.某地西红柿从2月1日起开始上市,通过市场调查,得到西红柿种植成本Q(单位:元/ kg)与上市时间t(单位:天)的数据如下
kg)与上市时间t(单位:天)的数据如下 表:
表:
| 时间t |
50 |
110 |
250 |
| 种植成本Q |
150 |
108 |
150 |
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本Q与上市时间t的变化关系,并说明选取该函数的理由。 ,
, ,
, ,
,
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本。
.函数 (
( 为实常数).
为实常数).
(1)若 ,求
,求 的单调区间;
的单调区间;
(2)若 ,设
,设 在区间
在区间 的最小值为
的最小值为 ,求
,求 的表达式
的表达式
设 其中
其中 .
.
(1)求 的取值范围;
的取值范围;
(2)若 ,
, ,求
,求 的值.
的值.
.阅读与理解:
给出公式: ;
; ;
;
我们可以根据公式将函数 化为:
化为:
(1)根据你的理解将函数 化为
化为 的形式.
的形式.
(2)求出上题函数 的最小正周期、对称中心.
的最小正周期、对称中心.
(3)求函数在区间 上的最大值、最小值及相应的
上的最大值、最小值及相应的 的值。
的值。
集合 和
和 ,若
,若 ,
, ,分别求实数p、a、b的值。
,分别求实数p、a、b的值。