阅读下列材料:
2015年清明小长假,北京市属公园开展以“清明踏青,春色满园”为主题的游园活动,虽然气温小幅走低,但游客踏青赏花的热情很高,市属公园游客接待量约为190万人次,其中,玉渊潭公园的樱花、北京植物园的桃花受到了游客的热捧,两公园的游客接待量分别为28万人次、21.75万人次;颐和园、天坛公园、公园因皇家园林的厚重文化底蕴与满园春色成为游客的重要目的地,游客接待量分别为26万人次、20万人次、17.6万人次;北京动物园游客接待量为18万人次,熊猫馆的游客密集度较高.
2014年清明小长假,天气晴好,北京市属公园游客接待量约为200万人次,其中,玉渊潭公园游客接待量比2013年清明小长假增长了25%;颐和园游客接待量为26.2万人次,比2013年清明小长假增加了4.6万人次;北京动物园游客接待量为22万人次.
2013年清明小长假,玉渊潭公园、陶然亭公园、北京动物园游客接待量分别为32万人次,13万人次、14.9万人次.
根据以上材料解答下列问题:
(1)2014年清明小长假,玉渊潭公园游客接待量为____万人次;
(2)选择统计表或统计图,将2013-2015年清明小长假玉渊潭公园、颐和园和北京动物园的游客接待量表示出来.
(乐山)如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.
(巴中)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(项点是网格线的交点).
(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)线段B1C1变换到B1C2的过程中扫过区域的面积为 .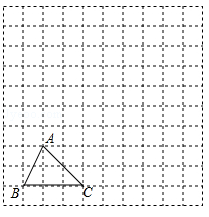
(广安)在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O,求证:OA=OE.
(绵阳)如图,反比例函数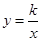 (
( )与正比例函数
)与正比例函数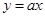 相交于A(1,k),B(﹣k,﹣1)两点.
相交于A(1,k),B(﹣k,﹣1)两点.
(1)求反比例函数和正比例函数的解析式;
(2)将正比例函数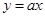 的图象平移,得到一次函数
的图象平移,得到一次函数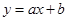 的图象,与函数
的图象,与函数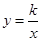 (
( )的图象交于C(
)的图象交于C(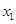 ,
,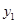 ),D(
),D(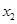 ,
, ),且
),且 ,求b的值.
,求b的值.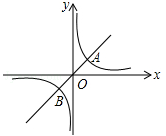
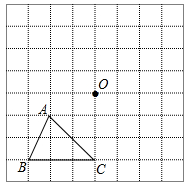
(眉山)(本小题满分8分)如图,在方格网中已知格点△ABC和点C.
(1)画 和△ABC关于点O成中心对称;
和△ABC关于点O成中心对称;
(2)请在方格网中标出所有使以点A、O、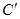 、D为顶点的四边形是平行四边形的D点.
、D为顶点的四边形是平行四边形的D点.