(绵阳)如图,反比例函数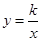 (
( )与正比例函数
)与正比例函数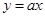 相交于A(1,k),B(﹣k,﹣1)两点.
相交于A(1,k),B(﹣k,﹣1)两点.
(1)求反比例函数和正比例函数的解析式;
(2)将正比例函数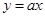 的图象平移,得到一次函数
的图象平移,得到一次函数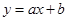 的图象,与函数
的图象,与函数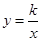 (
( )的图象交于C(
)的图象交于C(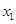 ,
,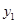 ),D(
),D(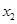 ,
, ),且
),且 ,求b的值.
,求b的值.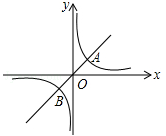
解下列方程
①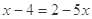
②解方程: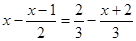
解:去分母,得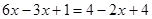 ……①
……①
即 ……②
……②
移项,得 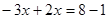 ……③
……③
合并同类项,得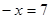 ……④
……④
∴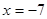 ……⑤
……⑤
上述解方程的过程中,是否有错误?答:__________;如果有错误,则错在__________步。如果上述解方程有错误,请你给出正确的解题过程:
③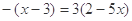
④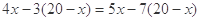
如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.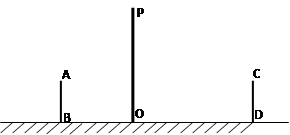
(1)在小亮由B处沿BO所在的方向行走到达O处的过程中,他在地面上的影子长度的变化情况为 ;
(2)请你在图中画出小亮站在AB处的影子;
(3)当小亮离开灯杆的距离OB=4.2m时,身高(AB)为1.6m的小亮的影长为1.6m,问当小亮离开灯杆的距离OD=6m时,小亮的影长是多少m?
画右边几何体的三种视图(注意符合三视图原则).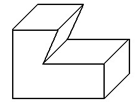
(2014中考真题)某小商场以每件20元的价格购进一种服装,先试销一周,试销期间每天的销量(件)与每件的销售价x(元/件)如下表:
| x(元/件) |
38 |
36 |
34 |
32 |
30 |
28 |
26 |
| t(件) |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
(1)试求t与x之间的函数关系式;
(2)在商品不积压且不考虑其它因素的条件下,每件服装的销售定价为多少时,该小商场销售这种服装每天获得的毛利润最大?每天的最大毛利润是多少?(注:每件服装销售的毛利润=每件服装的销售价-每件服装的进货价)
如图,在平面直角坐标系中,抛物线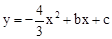 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.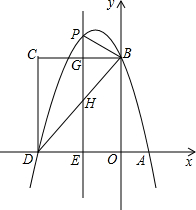
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.