先化简,再求值: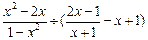 ,其中
,其中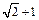 .
.
计算:
(1)如图1,在平行四边形ABCD中,∠A=30°,AB=6,AD=8,将平行四边形ABCD分割成两部分,然后拼成一个矩形,请画出拼成的矩形,并说明矩形的长和宽.(保留分割线的痕迹)
(2)若将一边长为1的正方形按如图2﹣1所示剪开,恰好能拼成如图2﹣2所示的矩形,则m的值是多少?
(3)四边形ABCD是一个长为7,宽为5的矩形(面积为35),若把它按如图3﹣1所示的方式剪开,分成四部分,重新拼成如图3﹣2所示的图形,得到一个长为9,宽为4的矩形(面积为36).问:重新拼成的图形的面积为什么会增加?请说明理由.

某种机器使用若干年后即被淘汰,该机器有一易损零件,为调查该易损零件的使用情况,随机抽取了100台已被淘汰的这种机器,经统计:每台机器在使用期内更换的该易损零件数均只有8,9,10,11这四种情况,并整理了这100台机器在使用期内更换的该易损零件数,绘制成如图所示不完整的条形统计图.
(1)请补全该条形统计图;
(2)某公司计划购买一台这种机器以及若干个该易损零件,用上述100台机器更换的该易损零件数的频率代替一台机器更换的该易损零件数发生的概率.
①求这台机器在使用期内共更换了9个该易损零件的概率;
②若在购买机器的同时购买该易损零件,则每个200元;若在使用过程中,因备用该易损零件不足,再购买,则每个500元.请你帮该公司用花在该易损零件上的费用的加权平均数进行决策:购买机器的同时应购买几个该易损零件,可使公司的花费最少?

如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.

如图,已知⊙O是△ABC的外接圆,且BC为⊙O的直径,在劣弧 上取一点D,使 ,将△ADC沿AD对折,得到△ADE,连接CE.
(1)求证:CE是⊙O的切线;
(2)若CE CD,劣弧 的弧长为π,求⊙O的半径.
