在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的反称点的定义如下：若在射线CP上存在一点P′，满足CP＋CP′＝2r.则称P′为点P关于⊙C的反称点，下图为点P及其关于⊙C的反称点P′的示意图.
特别地，当点P′与圆心C重合时，规定CP′＝0.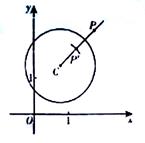
（1）当⊙O的半径为1时.
①分別判断点M（2，1），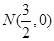
，
关于⊙O的反称点是否存在？若存在，求其坐标；
②点P在直线y＝－x＋2上，若点P关于⊙O的反称点P′存在，且点P′不在x袖上，求点P的横坐标的取值范围；
（2）⊙C的圆心在x袖上，半径为1，直线
与x轴、y轴分別交于点A，B.若线段AB存在点P，使得点P关于⊙C的反称点P′在⊙C的内部，求圆心C的横坐标的取值范围.
如图，在△ABC中，∠C=900 ，DE垂直平分AB，分别交AB,BC于D,E。若∠CAE=∠B+300 ,求∠AEB 的度数
如图，AB=DE,BE=CF,AB∥DE求证：∠A=∠D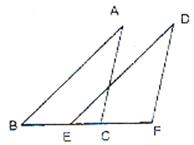
先化简，再求值：
,其中x=-1,y=2.
分解因式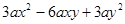 
在平面直角坐标系xoy中，边长为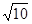
的正方形ABCD的对角线AC、BD相交于点P，顶点A在x轴正半轴上运动，顶点B在y轴正半轴上运动（x轴的正半轴、y轴的正半轴都不包含原点O），顶点C、D都在第一象限．
⑴当∠BAO=45°时，求点P的坐标;
⑵求证：无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动，点P都在∠AOB的平分线上；
⑶当B点坐标为（0,1）时，求CD的解析式。