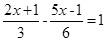如图，在离水面高度为5米的岸上有人用绳子拉船靠岸，开始时绳子与水面的夹角为30°，此人以每秒0.5米的速度收绳．问：
（1）未开始收绳子的时候，图中绳子BC的长度是多少米？
（2）收绳8秒后船向岸边移动了多少米？（结果保留根号）
小红在做一道题:已知两个多项式A,B,A=
,计算A+2B时,她误将 A+2B写成2A+B,算出的结果是
.请你帮她计算出正确结果。
一根80厘米的弹簧，一端固定，如果另一端挂上物体，那么在正常情况下物体的质量每增加1千克可使弹簧增长2厘米。（10 分）
（1）填写下表
| 所挂物体的质量（千克） |
1 |
2 |
3 |
4 |
… |
| 弹簧的总长度（厘米） |
… |
（2）写出弹簧总长度y（厘米）与所挂物体的质量x（千克）之间的数量关系。
（3）若在这根弹簧上挂上某一物体后，弹簧总长为96 厘米，求所挂物体的质量？
已知线段AB="10cm" ，射线AB上有一点C，且BC=4cm，M是线段AC的中点，求线段AM的长？
用直尺和圆规作一个角等于∠MON
。（不写步骤，保留作图痕迹）
用直尺和圆规作一个角等于∠MON。（不写步骤，保留作图痕迹）
（1）
（2）