已知矩形ABCD的一条边AD＝8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．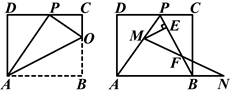
（1）如图1，已知折痕与边BC交于点O，连接AP、OP、OA．
①求证：△OCP∽△PDA；
②若△OCP与△PDA的面积比为1︰4，求边AB的长；
（2）若图1中的点P恰好是CD边的中点，求∠OAB的度数；
（3）如图2，在（1）的条件下，擦去折痕AO、线段OP，连接BP．动点M在线段AP上（点M与点P、A不重合），动点N在线段AB的延长线上，且BN＝PM，连接MN交PB于点F，作ME⊥BP于点E．试问当点M、N在移动过程中，线段EF的长度是否发生变化？若变化，说明理由；若不变，求出线段EF的长度．
抗震救灾抢修损坏的桥梁工程必须在规定日期内完成，保证救灾物质顺利通过。如果甲工程队单独做正好如期完成；若乙工程队单独做需要超过4天才能完成。现由甲、乙两队合作3天，余下的工程由乙队单独做正好按期完成，问规定日期是多少天？
已知一次函数与反比例函数的图象相交于点A(1,-2)和Q(m,1)求这两个函数的关系式
在同一坐标系中画出这两个函数的图象，根据图象回答：当x为何值时，一次函数的值小于反比例函数的值？
已知：在△ABC中，∠CAB=
，且
，AP平分∠CAB．如图1，若
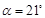，∠ABC=32°，且AP交BC于点P，试探究线段
AB，AC与PB之间的数量关系，并对你的结论加以证明；
答：线段AB，AC与PB之间的数量关系为：___________________________．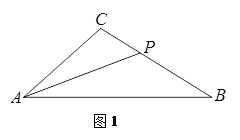
如图2，若∠ABC=
，点P在△ABC的内部，且使∠CBP=30°，
求∠APC的度数（用含
的代数式表示）
有甲、乙两个均装有进水管和出水管的容器，水管的所有阀门都处于关闭状态．
初始时，同时打开甲、乙两容器的进水管，两容器都只进水；
到8分钟时，关闭甲容器的进水管，打开它的出水管，甲容器只出水；
到16分钟时，再次打开甲容器的进水管，此时甲容器既进水又出水；
到28分钟时，关闭甲容器的出水管，并同时关闭甲、乙两容器的进水管．
已知两容器每分钟的进水量与出水量均为常数，图中折线O-A-B-C和线段DE分别表示两容器内的水量
(单位：升)与时间
(单位：分)之间的函数关系，请根据图象回答下列问题
甲容器的进水管每分钟进水______升，它的出水管每分钟出水______升；
求乙容器内的水量
与时间的函数关系式求从初始时刻到最后一次两容器内的水量相等时所需的时间．
已知：如图，在△ABC中，AB=AC，∠BAC=30°．点D为△ABC内一点，
且DB=DC，∠DCB=30°．点E为BD延长线上一点，且AE=AB
求∠ADE的度数
若点M在DE上，且DM=DA，
求证：ME=DC．