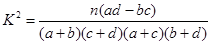(本小题满分12分)某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗 原料1千克、
原料1千克、 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗 原料2千克,
原料2千克,  原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗
原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗 、
、 原料都不超过12千克.如何合理安排生产计划,使公司可获得最大利润?最大利润为多少?
原料都不超过12千克.如何合理安排生产计划,使公司可获得最大利润?最大利润为多少?
已知等差数列{ }中,
}中, ,前
,前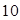 项和
项和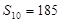 .
.
(1)求通项 ;
;
(2)若从数列{ }中依次取第
}中依次取第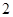 项、第
项、第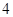 项、第
项、第 项…第
项…第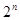 项……按原来的顺序组成一个新的数列{
项……按原来的顺序组成一个新的数列{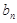 },求数列{
},求数列{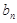 }的前
}的前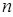 项和
项和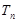 .
.
已知ΔABC的角A、B、C所对的边分别是a、b、c,设向量 ,
, ,
,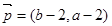 .
.
(1)若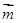 //
// ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形;
(2)若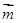 ⊥
⊥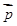 ,边长
,边长 ,角
,角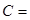
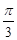 ,求ΔABC的面积 .
,求ΔABC的面积 .
已知 是定义在区间
是定义在区间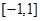 上的奇函数,且
上的奇函数,且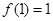 ,若
,若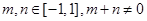 时,有
时,有 .
.
(1)解不等式: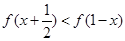 ;
;
(2)若不等式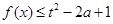 对
对 与
与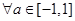 恒成立,求实数
恒成立,求实数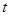 的取值范围.
的取值范围.
已知函数 .
.
(1)画出该函数的图像;
(2)设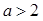 ,求
,求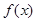 在
在 上的最大值.
上的最大值.
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
| 性别 是否需要志愿者 |
男 |
女 |
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有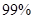 的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中需要志愿者提供帮助的老年人的比例?说明理由.
附:
 |
0.050 |
0.010 |
0.001 |
 |
3.841 |
6.635 |
10.828 |