如图，某仓储中心有一斜坡AB，其坡度为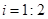
，顶部A处的高AC为4m，B、C在同一水平地面上。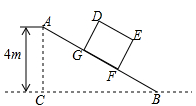
（1）求斜坡AB的水平宽度BC；
（2）矩形DEFG为长方形货柜的侧面图，其中DE=2.5m，EF=2m.将该货柜沿斜坡向上运送，当BF=3.5m时，求点D离地面的高。（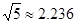
，结果精确到0.1m）
勾股定理是一条古老的数学定理，它有很多种证明方法，我国汉代数学家赵爽根据弦图，利用面积法进行证明，著名数学家华罗庚曾提出把“数形关系”（勾股定理）带到其他星球，作为地球人与其他星球“人”进行第一次“谈话”的语言．
[定理表述]
请你根据图1中的直角三角形，写出勾股定理内容；
[尝试证明]
以图1中的直角三角形为基础，可以构造出以a、b为底，以a+b为高的直角梯形（如图2），请你利用图2，验证勾股定理．
如图，如图，在△ABC中，AD⊥BC于D，∠ABC=2∠C，求证：AC2=AB2+AB•BC．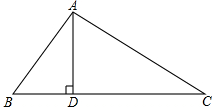
在直角三角形中，如果两直角边之和为17，两直角边之差的平方为49，求斜边的长。
如图，在四边形ABCD中，AB=8，BC=1，∠DAB=30°，∠ABC=60°，四边形ABCD的面积为5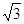
，求AD的长。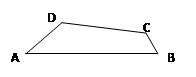
在△ABC中，∠C=Rt∠，BC=a，AC=b，AB=c。
（1）a=9，b=12，求c；
（2）a=9，c=41，求b；
（3）a=11，b=13，求以c为边的正方形的面积。