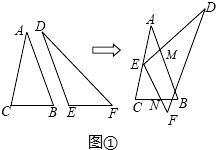
如图,△ABC中,AB=5,BC=4,∠B=50°,△A′B′C′中,A′B′=6,B′C′=4.8,∠B′=50°,AD,A′D′分别是边BC,B′C′上的高,AE,A′E′分别是∠BAC,∠B′A′C′的平分线.
(1)△ABC与△A′B′C′相似吗?请说明理由.
(2)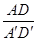 等于多少?
等于多少?
(3)若AE=4.5,那么A′E′等于多少?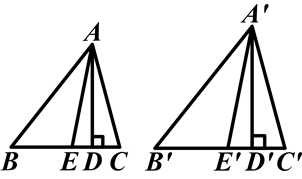
(年湖南娄底10分)如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连
接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?
(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值;′
(3)当t为何值时,△APQ是等腰三角形?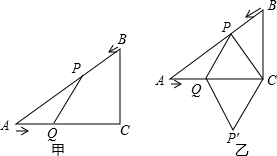
(年湖南怀化10分)如图1,在平面直角坐标系中,AB=OB=8,∠ABO=90°,∠yOC=45°,射线OC以每秒2个单位长度的速度向右平行移动,当射线OC经过点B时停止运动,设平行移动x秒后,射线OC扫过Rt△ABO的面积为y.
(1)求y与x之间的函数关系式;
(2)当x=3秒时,射线OC平行移动到O′C′,与OA相交于G,如图2,求经过G,O,B三点的抛物线的解析式;
(3)现有一动点P在(2)中的抛物线上,试问点P在运动过程中,是否存在三角形POB的面积S=8的情况?若存在,求出点P的坐标,若不存在,请说明理由.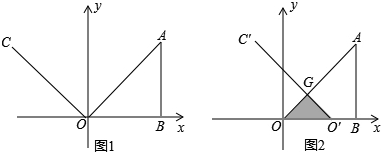
(年湖南衡阳10分)如图,已知直线AB分别交x轴、y轴于点A(﹣4,0)、B(0,3),点P从点A出发,以每秒1个单位的速度沿直线AB向点B移动,同时,将直线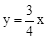 以每秒0.6个单位的速度向上平移,分别交AO、BO于点C、D,设运动时间为t秒(0<t<5).
以每秒0.6个单位的速度向上平移,分别交AO、BO于点C、D,设运动时间为t秒(0<t<5).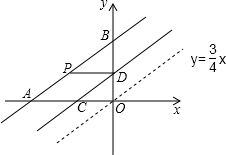
(1)证明:在运动过程中,四边形ACDP总是平行四边形;
(2)当t取何值时,四边形ACDP为菱形?且指出此时以点D为圆心,以DO长为半径的圆与直线AB的位置关系,并说明理由.
(年湖北黄冈13分)如图,在四边形OABC中,AB∥OC,BC⊥x轴于C,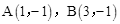 ,动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.过P作PQ⊥OA于Q.设P点运动的时间为t秒(0 < t < 2),ΔOPQ与四边形OABC重叠的面积为S.
,动点P从O点出发,沿x轴正方向以2个单位/秒的速度运动.过P作PQ⊥OA于Q.设P点运动的时间为t秒(0 < t < 2),ΔOPQ与四边形OABC重叠的面积为S.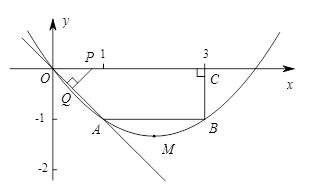
(1)求经过O、A、B三点的抛物线的解析式并确定顶点M的坐标;
(2)用含t的代数式表示P、Q两点的坐标;
(3)将ΔOPQ绕P点逆时针旋转90°,是否存在t,使得ΔOPQ的顶点O或Q落在抛物线上?若存在,直接写出t的值;若不存在,请说明理由;
(4)求S与t的函数解析式.
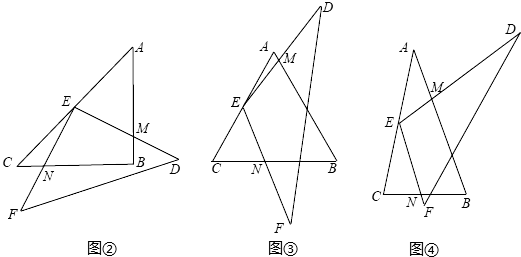
(年湖北江汉油田、潜江、天门、仙桃10分)如图①,△ABC与△DEF是将△ACF沿过A点的某条直线剪开得到的(AB,DE是同一条剪切线).平移△DEF使顶点E与AC的中点重合,再绕点E旋转△DEF,使ED,EF分别与AB,BC交于M,N两点.
(1)如图②,△ABC中,若AB=BC,且∠ABC=90°,则线段EM与EN有何数量关系?请直接写出结论;
(2)如图③,△ABC中,若AB=BC,那么(1)中的结论是否还成立?若成立,请给出证明:若不成立,请说明理由;
(3)如图④,△ABC中,若AB:BC=m:n,探索线段EM与EN的数量关系,并证明你的结论.