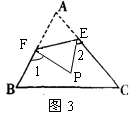
已知:如图所示,PN∥BC,AD⊥BC交PN于E,交BC于D.
(1)若AP︰PB=1︰2,S△ABC=18,求S△APN的值;
(2)若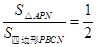 ,求
,求 的值;
的值;
(3)若BC=15,AD=10,且PN=ED=x,求x的值.
由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图)。请你用两种不同的方法分别在图中再将两个空白的小正方形涂黑,使它成为轴对称图形。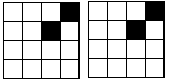
化简求值: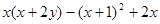 ,其中
,其中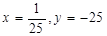
化简: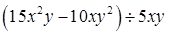
计算: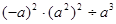
探索归纳:
(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于( )
| A.90° | B.135° | C.270° | D.315° |
(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=_______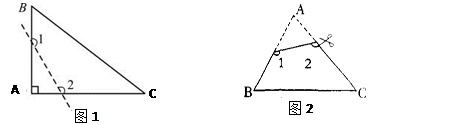
(3)如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是________________
(4)如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.