甲、乙两人在100米直道AB上练习匀速往返跑，若甲、乙分别中A，B两端同时出发，分别到另一端点处掉头，掉头时间不计，速度分别为5m/s和4m/s．
（1）在坐标系中，虚线表示乙离A端的距离s（单位：m）与运动时间t（单位：s）之间的函数图象（0≤t≤200），请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象（0≤t≤200）；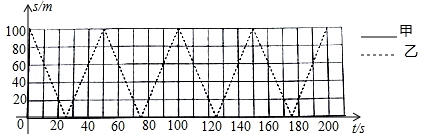
（2）根据（1）中所画图象，完成下列表格：
（3）①直接写出甲、乙两人分别在第一个100m内，s与t的函数解析式，并指出自变量t的取值范围；
②当t=390s时，他们此时相遇吗？若相遇，应是第几次？若不相遇，请通过计算说明理由，并求出此时甲离A端的距离．
如图，在Rt△ABC中，∠C=90°，AC=8，∠A的平分线AD=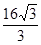
，求∠B的度数及边BC、AB的长.
根据下列条件，求出Rt△ABC(∠C=90°)中未知的边和锐角.
（1）BC=8，∠B=60°；（2）AC=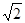
，AB=2.
计算：6tan2 30°－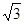
sin 60°－2sin 45°.
计算：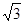
cos30°+
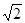sin45°；
如图，抛物线y＝
x2－
x－12与x轴交于A、C两点，与y轴交于B点．
（1）求△AOB的外接圆的面积；
（2）若动点P从点A出发，以每秒2个单位沿射线AC方向运动；同时，点Q从点B出发，以每秒1个单位沿射线BA方向运动，当点P到达点C处时，两点同时停止运动。问当t为何值时，以A、P、Q为顶点的三角形与△OAB相似？
（3）若M为线段AB上一个动点，过点M作MN平行于y轴交抛物线于点N．
①是否存在这样的点M，使得四边形OMNB恰为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．
②当点M运动到何处时，四边形CBNA的面积最大？求出此时点M的坐标及四边形CBAN面积的最大值．