(本小题满分12分)已知正项数列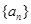 的首项
的首项 ,前
,前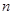 项和
项和 满足
满足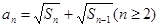 .
.
(Ⅰ)求证: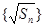 为等差数列,并求数列
为等差数列,并求数列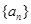 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前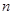 项和为
项和为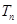 ,若对任意的
,若对任意的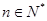 ,不等式
,不等式 恒成立,求实数
恒成立,求实数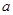 的取值范围.
的取值范围.
已知抛物线 ,其焦点为F,一条过焦点F,倾斜角为
,其焦点为F,一条过焦点F,倾斜角为
 的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点
的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点 ,连接BO,交准线于点
,连接BO,交准线于点 ,求四边形
,求四边形 的面积.
的面积.
给定圆P: 及抛物线S:
及抛物线S: ,过圆心
,过圆心 作直线
作直线 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为 ,如果线段
,如果线段 的长按此顺序构成一个等差数列,求直线l的方程.
的长按此顺序构成一个等差数列,求直线l的方程.
已知半径为1的定圆⊙P的圆心P到定直线 的距离为2,Q是
的距离为2,Q是 上一动点,⊙Q与⊙P相外切,⊙Q交
上一动点,⊙Q与⊙P相外切,⊙Q交 于M、N两点,对于任意直径MN,平面上恒有一定点A,使得∠MAN为定值。求∠MAN的度数。
于M、N两点,对于任意直径MN,平面上恒有一定点A,使得∠MAN为定值。求∠MAN的度数。
椭圆 的右焦点为F,P1,P2,…,P24为24个依逆时针顺序排列在椭圆上的点,其中P1是椭圆的右顶点,并且∠P1FP2=∠P2FP3=∠P3FP4=…=∠P24FP1.若这24个点到右准线的距离的倒数和为S,求S2的值.
的右焦点为F,P1,P2,…,P24为24个依逆时针顺序排列在椭圆上的点,其中P1是椭圆的右顶点,并且∠P1FP2=∠P2FP3=∠P3FP4=…=∠P24FP1.若这24个点到右准线的距离的倒数和为S,求S2的值.
在 轴同侧的两个圆:动圆
轴同侧的两个圆:动圆 和圆
和圆 外切(
外切( ),且动圆
),且动圆 与
与 轴相切,求(1)动圆
轴相切,求(1)动圆 的圆心轨迹方程L;(2)若直线
的圆心轨迹方程L;(2)若直线 与曲线L有且仅有一个公共点,求
与曲线L有且仅有一个公共点,求 之值。
之值。