从某批产品中,有放回地抽取产品两次,每次随机抽取1件,假设事件 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率 .
.
(Ⅰ)求从该批产品中任取1件是二等品的概率 ;
;
(Ⅱ)若该批产品共20件,从中任意抽取2件,X表示取出的2件产品中二等品的件数,求X的分布列与期望.
(本题满分14分
已知椭圆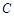 :
: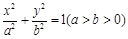 的离心率为
的离心率为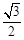 ,以原点为圆心,
,以原点为圆心,
椭圆的短半轴长为半径的圆与直线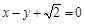 相切.
相切.
⑴求椭圆C的方程;
⑵设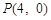 ,
,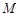 、
、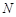 是椭圆
是椭圆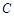 上关于
上关于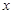 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结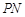 交椭圆
交椭圆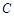
于另一点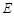 ,求直线
,求直线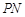 的斜率的取值范围;
的斜率的取值范围;
⑶在⑵的条件下,证明直线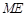 与
与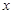 轴相交于定点.
轴相交于定点.
在数列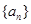 中,
中,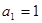 ,
,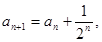 ,
,
(1)求数列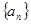 的通项公式;
的通项公式;
(2)求数列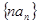 的前
的前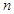 项和
项和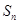 ;
;
(3)在(2)的条件下指出数列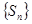 的最小项的值,并证明你的结论。
的最小项的值,并证明你的结论。
如图, 在直三棱柱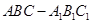 中,
中,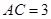 ,
,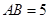 ,
,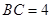
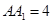 ,点
,点 是
是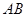 的中点.
的中点.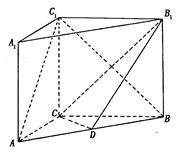
⑴求证: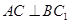 ;
;
⑵求证: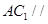 平面
平面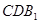 ;
;
⑶求二面角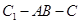 的正切值.
的正切值.
甲、乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,
答错得零分.假设甲队中每人答对的概率均为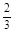 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为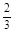 ,
,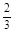 ,
,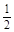 ,且各人回答正确与否相互之间没有影响.用
,且各人回答正确与否相互之间没有影响.用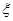 表示甲队的总得分.
表示甲队的总得分.
(1)求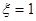 的概率及
的概率及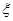 的数学期望
的数学期望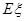 ;
;
(2)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求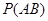 .
.
已知:△ABC中角A、B、C所对的边分别为
且 .
.
(1)求角C的大小;
(2)若 成等差数列,且
成等差数列,且 ,求边
,求边 的长.
的长.