关于函数f(x)=4sin(2x+ ), (x∈R)有下列结论:
), (x∈R)有下列结论:
①y=f(x)是以π为最小正周期的周期函数;
②y=f(x)可改写为y=4cos(2x- );
);
③y=f(x)的最大值为4;
④y=f(x)的图象关于直线x=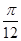 对称;
对称;
则其中正确结论的序号为 .
连掷两次骰子分别得到点数m,n,则向量(m,n)与向量(-1,1)的夹角θ>90°的概率是__________.
一对年轻夫妇和其两岁的孩子做游戏,让孩子把分别写有“1”“3”“1”“4”的四张卡片随机排成一行,若卡片按从左到右的顺序排成“1314”,则孩子会得到父母的奖励,那么孩子得到奖励的概率为__________.
在区间[0,4]内随机取两个数a,b,则使得函数f(x)=x2+ax+b2有零点的概率为________.
从一批产品中取出三件产品,设A={三件产品全不是次品},B={三件产品全是次品},C={三件产品不全是次品},则下列结论正确的序号是________.
①A与B互斥;②B与C互斥;③A与C互斥;④A与B对立;⑤B与C对立.
在2014年元旦期间,某市物价部门对本市五个商场销售的某商品一天的销售量及其价格进行调查,五个商场的售价x元和销售量y件之间的一组数据如表所示:
| 价格x |
9 |
9.5 |
10 |
10.5 |
11 |
| 销售量y |
11 |
10 |
8 |
6 |
5 |
通过分析,发现销售量y与商品的价格x具有线性相关关系,则销售量y关于商品的价格x的线性回归方程为__________.