如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.20T,方向垂直纸面向里,电场强度E1=1.0×105V/m,PQ为板间中线。紧靠平行板右侧边缘 坐标系的第一象限内,有一边界AO、与y轴的夹角∠
坐标系的第一象限内,有一边界AO、与y轴的夹角∠ =450,边界线的上方有垂直纸面向外的匀强磁场,磁感应强度B2=0.25T,边界线的下方有竖直向上的匀强电场,电场强度E2=5.0×105V/m。一束带电荷量q=8.0×10-19C、质量m=8.0×10-26Kg的正离子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从
=450,边界线的上方有垂直纸面向外的匀强磁场,磁感应强度B2=0.25T,边界线的下方有竖直向上的匀强电场,电场强度E2=5.0×105V/m。一束带电荷量q=8.0×10-19C、质量m=8.0×10-26Kg的正离子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从 轴上坐标为(0,0.4 m)的Q点垂直
轴上坐标为(0,0.4 m)的Q点垂直 轴射入磁场区,多次穿越边界线OA。求:
轴射入磁场区,多次穿越边界线OA。求:
(1)离子运动的速度;
(2)离子从进入磁场到第二次穿越边界线OA所需的时间;
(3)离子第四次穿越边界线的位置坐标。
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点。试求: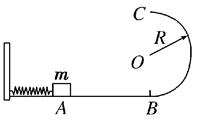
(1)弹簧开始时的弹性势能;
(2)物体从B点运动至C点克服阻力做的功;
(3)物体离开C点后落回水平面时的速度大小和方向。
在真空中,半径为r的圆形区域内存在垂直纸面向外的匀强磁场,磁感应强度大小为B,在此区域外围空间有垂直纸面向内的磁感应强度大小也为B的匀强磁场.一个带电粒子从边界上的P点沿半径向外,以速度v0进入外围磁场,已知带电粒子质量m=2×10-10kg,带电荷量q=+5×10-6 C,不计重力,磁感应强度B=1 T,粒子运动速度v0=5×103 m/s,圆形区域半径r=0.2 m,求粒子第一次回到P点所需时间.(结果用π表示)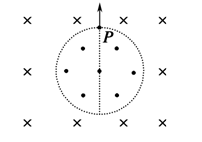
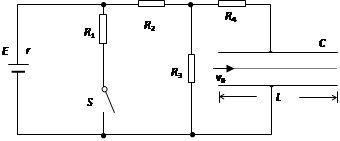
一电路如图所示,电源电动势 ,内阻
,内阻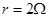 ,电阻
,电阻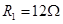 ,
,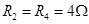 ,
,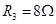 ,C为平行板电容器,其电容C=3.0pF,虚线到两极板距离相等,极板长
,C为平行板电容器,其电容C=3.0pF,虚线到两极板距离相等,极板长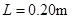 ,两极板的间距
,两极板的间距 。
。
(1)若开关S处于断开状态,则当其闭合后,求流过R4的总电量为多少?
(2)若开关S断开时,有一带电微粒沿虚线方向以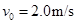 的初速度射入C的电场中,刚好沿虚线匀速运动,问:当开关S闭合后,此带电微粒以相同初速度沿虚线方向射入C的电场中,能否从C的电场中射出?(要求写出计算和分析过程,g取
的初速度射入C的电场中,刚好沿虚线匀速运动,问:当开关S闭合后,此带电微粒以相同初速度沿虚线方向射入C的电场中,能否从C的电场中射出?(要求写出计算和分析过程,g取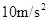 )
)
水上滑梯可简化成如图所示的模型,斜槽AB和水平槽BC平滑连接,斜槽AB的竖直高度H=6.0m,倾角θ=37º.水平槽BC长d=2.0m,BC面与水面的距离h=0.80m,人与AB、BC间的动摩擦因数均为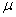 =0.10.取重力加速度g=10m/s2,cos 37º="0.8,sin" 37º=0.6.一小朋友从滑梯顶端A点无初速地自由滑下,求:
=0.10.取重力加速度g=10m/s2,cos 37º="0.8,sin" 37º=0.6.一小朋友从滑梯顶端A点无初速地自由滑下,求: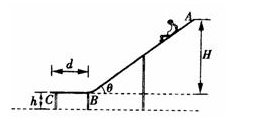
(1)小朋友沿斜槽AB下滑时加速度的大小a;
(2)小朋友滑到C点时速度的大小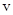 ;
;
(3)在从C点滑出至落到水面的过程中,小朋友在水平方向位移的大小x。
汽车在平直的公路上以10m/s的速度做匀速直线运动,发现前面有情况而刹车,若获得的加速度大小为2m/s2,则在8s末汽车的速度有多大?