弗林特的珍宝曾隐藏在不同的岛上,并且对藏宝地点不止一次利用坐标法.如图中画着岛的地图,在其上有两个标记(两块大石头).现今的寻宝者没有原来的地图,但是他们知道,在该图上大石头的坐标A(2,1),B(8,2),而藏宝地的坐标是 ,
, ,在地图上找出宝藏的地点.
,在地图上找出宝藏的地点.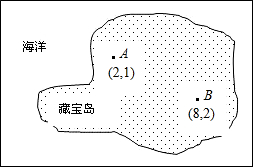
某班教室中有9排5列座位,请根据下面四个同学的描述,在图中标出“5号”小明的位置.1号同学说:“小明在我的右后方.”2号同学说:“小明在我的左后方.”3号同学说:“小明在我的左前方.”4号同学说:“小明离1号同学和3号同学的距离一样远.”
如图,是一个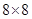 的球桌,小明用
的球桌,小明用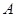 球撞击
球撞击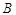 球,到
球,到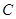 处反弹,再撞击桌边
处反弹,再撞击桌边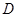 处,请选择适当的直角坐标系,并用坐标表示各点的位置.
处,请选择适当的直角坐标系,并用坐标表示各点的位置.
如图是小青所在学校的平面示意图,请你建立适当的坐标系描述食堂的位置.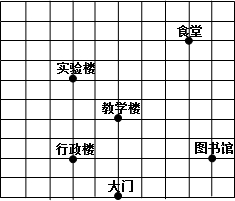
如图是某动物园的平面示意图.借助刻度尺、量角器,解决如下问题:
⑴猴园和鹿场分别位于水族馆的什么位置?
⑵与水族馆距离相同的地方有哪些场地?
⑶如果用(5,3)表示图上的水族馆的位置,那么猛兽区怎样表示?(7,6)表示什么区?