为了解中考体育科目训练情况,某地从九年级学生中随机抽取了部分学生进行了一次考前体育科目测试,把测试结果分为四个等级: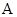 级:优秀;
级:优秀;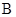 级:良好;
级:良好;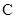 级:及格;
级:及格;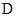 级:不及格,并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
级:不及格,并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题: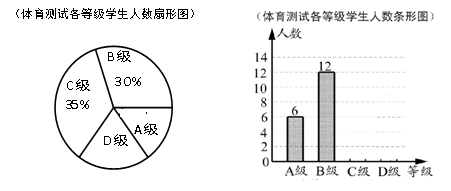
(1)请将两幅不完整的统计图补充完整;
(2)如果该地参加中考的学生将有4500名,根据测试情况请你估计不及格的人数有多少?
(3)从被抽测的学生中任选一名学生,则这名学生成绩是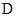 级的概率是多少?
级的概率是多少?
如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.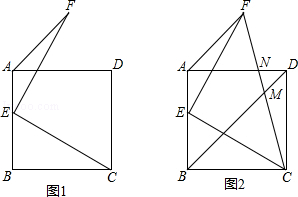
(1)求∠EAF的度数;
(2)如图2,连接FC交BD于M,交AD于N.
①求证: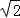 AD=AF+2DM;
AD=AF+2DM;
②若AF=10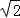 ,AN=12,则MD的长为 .
,AN=12,则MD的长为 .
A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台,已知从A市调运一台机器到C村和D村的运费分别是400元和800元,从B市调运一台机器到C村和D村的运费分别是300元和500元.
(1)设B市运往C村机器x台,求总运费W关于x的函数关系式;
(2)若要求总运费不超过9000元,共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少元?
分析由已知条件填出下表:
| 库存机器 |
支援C村 |
支援D村 |
| B市6台 |
x台 |
(6﹣x)台 |
| A市12台 |
(10﹣x)台 |
[8﹣(6﹣x)]台 |
如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.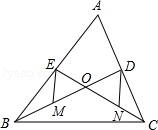
(1)求证:MD和NE互相平分;
(2)若BD⊥AC,EM=2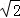 ,OD+CD=7,求△OCB的面积.
,OD+CD=7,求△OCB的面积.
今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.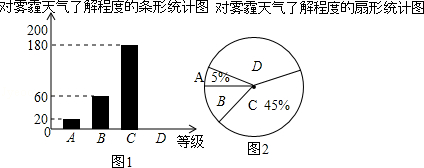
对雾霾了解程度的统计表:
对雾霾的了解程度 百分比
A.非常了解 5%
B.比较了解 m
C.基本了解 45%
D.不了解 n
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是多少度;
(3)请补全条形统计图.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3),△AOB关于y轴对称的图形为△A1OB1.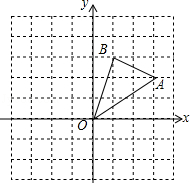
(1)画出△A1OB1并写出点B1的坐标为 ;
(2)写出△A1OB1的面积为 ;
(3)点P在x轴上,使PA+PB的值最小,写出点P的坐标为 .