(本小题满分12分)在数列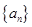 中,
中,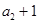 是
是 与
与 的等差中项,设
的等差中项,设 ,且满足
,且满足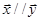 .
.
(1)求数列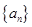 的通项公式;
的通项公式;
(2)记数列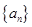 前
前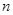 项的和为
项的和为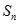 ,若数列
,若数列 满足
满足 ,试求数列
,试求数列 前
前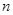 项的和
项的和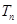 .
.
(本小题满分12分)在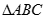 中,
中,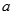 、
、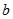 、
、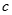 分别是三内角
分别是三内角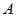 、
、 、
、 的对边,已知
的对边,已知 .
.
(1)求角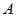 的大小;
的大小;
(2)若 ,求角
,求角 的大小.
的大小.
(本小题满分14分)已知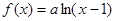 ,
,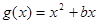 ,
,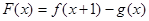 ,其中
,其中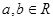 .
.
(1)若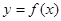 与
与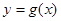 的图像在交点
的图像在交点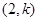 处的切线互相垂直,求
处的切线互相垂直,求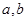 的值;
的值;
(2)若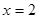 是函数
是函数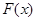 的一个极值点,
的一个极值点,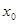 和
和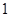 是
是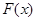 的两个零点,且
的两个零点,且 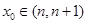 ,
,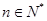 ,求
,求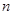 的值;
的值;
(3)当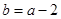 时,若
时,若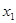 ,
,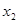 是
是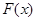 的两个极值点,当
的两个极值点,当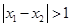 时,求证:
时,求证: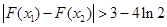 .
.
(本小题满分13分)已知函数 的导数为
的导数为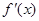 ,且数列
,且数列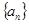 满足
满足 .
.
(1)若数列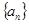 是等差数列,求
是等差数列,求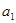 的值;
的值;
(2)当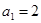 时,求数列
时,求数列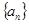 的前
的前 项和
项和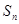 ;
;
(3)若对任意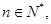 都有
都有 成立,求
成立,求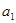 的取值范围.
的取值范围.
(本小题满分12分)北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估。该商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不
低于原收入,该商品每件定价最多为多少元?
(2)为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到 元.公司拟投入
元.公司拟投入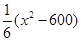 万作为技改费用,投入50万元作为固定宣传费用,投入
万作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品改革后的销售量
万元作为浮动宣传费用.试问:当该商品改革后的销售量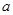 至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.