（本小题满分12分）设m∈R，在平面直角坐标系中，已知向量a＝（mx，y+1），向量b=（x，y-1），
，动点M（x，y）的轨迹为E．
（1）求轨迹E的方程，并说明该方程所表示曲线的形状;
（2）已知
，证明：存在圆心在原点的圆，使得该圆的任意一条切线与轨迹E恒有两个交点A，B，且OA⊥OB（O为坐标原点），并求该圆的方程。
设函数
．
（1）求
的最大值，并写出使取最大值时
的集合；
（2）已知
中，角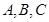
的对边分别为
，若
，
，求
的最小值．
已知函数
的最大值为3，函数
的图象上相邻两对称轴间的距离为
，且
．
（1）求函数的解析式；
（2）将的图象向左平移
个单位，再向下平移1个单位后得到函数
的图象，试判断的奇偶性，并求出在R上的单调递增区间．
已知数列
的前
项和为
．
（1）求数列的通项公式；
（2）求数列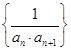
的前项和
的取值范围．
已知等比数列
中
，数列
满足
．
（1）求数列和的通项公式；
（2）设
，求数列
的前
项和
．
平面直角坐标系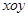
中，直线
的参数方程
（
为参数），圆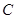
的方程为
，以坐标原点
为极点，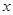
轴的非负半轴为极轴建立极坐标系．
（1）求直线和圆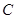的极坐标方程；
（2）求直线和圆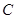的交点的极坐标（要求极角
）．