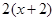如图,一次函数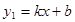 的图象与反比例函数
的图象与反比例函数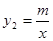 的图象相交于点A(2,3)
的图象相交于点A(2,3)
和点B,与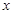 轴相交于点C(8,0) .
轴相交于点C(8,0) .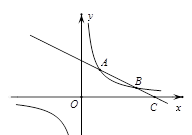
(1)求这两个函数的解析式;
(2)当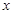 取何值时,
取何值时,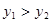 .
.
(本题10分)如果抛物线 过定点M(1,1),则称次抛物线为定点抛物线.
过定点M(1,1),则称次抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的一个解析式.小敏写出了一个答案: ,请你写出一个不同于小敏的答案;
,请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线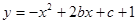 ,求该抛物线顶点纵坐标的值最小时的解析式,请你解答.
,求该抛物线顶点纵坐标的值最小时的解析式,请你解答.
(本题8分)如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).备用数据: ,
,
(本题8分)为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图.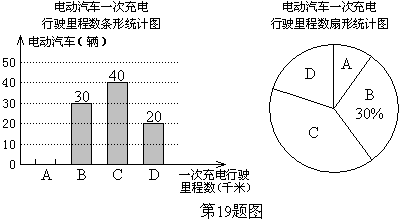
根据以上信息,解答下列问题:
(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;
(2)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
(本题8分)小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小敏离家的路程 (米)和所经过的时间
(米)和所经过的时间 之间的函数图象如图所示.请根据图象回答下列问题:
之间的函数图象如图所示.请根据图象回答下列问题:
(1)小敏去超市途中的速度是多少?在超市逗留了多少时间?
(2)小敏几点几分返回到家?
(本题8分)
(1)计算: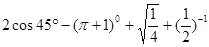 ;
;
(2)解不等式: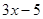 ≤
≤