如图所示,AB为竖直墙壁，A点和P点在同一水平面上。空间存在着竖直方向的匀强电场。将一带电小球从P点以速度v0向A抛出，结果打在墙上的C处。若撤去电场，将小球从P点以初速v0/2向A抛出，也正好打在墙上的C点。求：
（1）第一次抛出后小球所受电场力和重力之比
（2）小球两次到达C点时竖直速度之比
如图所示，一光滑斜面固定在水平地面上，质量m=lkg的物体在平行于斜面向上的恒力F作用下，从A点由静止开始运动，到达B点时立即撤去拉力F。此后，物体到达C点时速度为零。每隔0．2s通过传感器测得物体的瞬时速度，下表给出了部分测量数据。
| t/s |
0．0 |
0．2 |
0．4 |
… |
2．2 |
2．4 |
… |
| v/m·s-1 |
0．0 |
1．0 |
2．0 |
… |
3．3 |
2．1 |
… |
求：（1）恒力F的大小。
（2）撤去外力F的时刻。
如图甲所示，M和N是相互平行的金属板，OO1O2为中线，O1为板间区域的中点，P是足够大的荧光屏．带电粒子连续地从O点沿OO1方向射入两板间．
（1）若只在两板间加恒定电压U，M和N相距为d，板长为L（不考虑电场边缘效应）．若入射粒子是电量为e、质量为m的电子，试求能打在荧光屏P上偏离点O2最远的电子的动能．
（2）若两板间只存在一个以O1点为圆心的圆形匀强磁场区域，磁场方向垂直纸面向里，已知磁感应强度B=0．50T，两板间距d=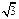
cm，板长L=1．0cm，带电粒子质量m=2．0×10-25kg，电量q=8．0×10-18C，入射速度v =
×105m/s．若能在荧光屏上观察到亮点，试求粒子在磁场中运动的轨道半径r，并确定磁场区域的半径R应满足的条件．
（3）若只在两板间加如图乙所示的交变电压u，M和N相距为d，板长为L（不考虑电场边缘效应）．入射粒子是电量为e、质量为m的电子．某电子在t0=
时刻以速度v0射入电场，要使该电子能通过平行金属板，试确定U0应满足的条件．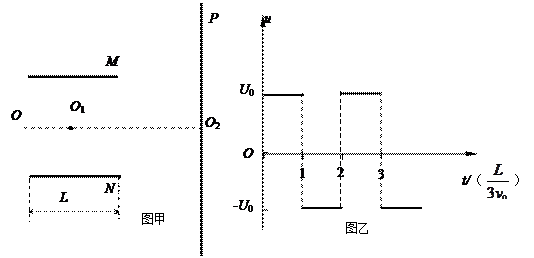
如图所示，固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷，电荷量分别为＋Q和－Q，A、B相距为2d。MN是竖直放置的光滑绝缘细杆，另有一个穿过细杆的带电小球p，质量为m、电荷量为+q（可视为点电荷，不影响电场的分布。），现将小球p从与点电荷A等高的C处由静止开始释放，小球p向下运动到距C点距离为d的O点时，速度为v。已知MN与AB之间的距离为d，静电力常量为k，重力加速度为g。求：
（1）C、O间的电势差UCO；
（2）O点处的电场强度E的大小及小球p经过O点时的加速度；
（3）小球p经过与点电荷B等高的D点时的速度。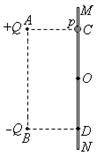
如图所示，半径为R=0．2m的光滑1/4圆弧AB在竖直平面内，圆弧B处的切线水平。B端高出水平地面h=0．8m，O点在B点的正下方。将一质量为m=1．0kg的滑块从A点由静止释放，落在水平面上的C点处，（g取10m/s2）求：
（1）滑块滑至B点时对圆弧的压力及xOC的长度；
（2）在B端接一长为L=1．0m的木板MN，滑块从A端释放后正好运动到N端停止，求木板与滑块的动摩擦因数μ。
（3）若将木板右端截去长为ΔL的一段，滑块从A端释放后将滑离木板落在水平面上P点处，要使落地点P距O点的最远，ΔL应为多少？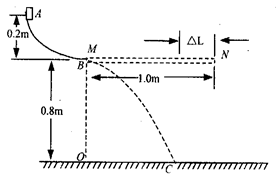
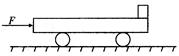
如图所示，质量M="8" kg的小车放在水平光滑的平面上，在小车左端加一水平推力F="8" N，当小车向右运动的速度达到1．5 m/s时，在小车前端轻轻地放上一个大小不计，质量为m="2" kg的小物块，物块与小车间的动摩擦因数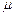
=0．2，小车足够长．（g取10m/s2），求
（1）小物块放后，小物块及小车的加速度各为多大？
（2）经多长时间两者达到相同的速度？
（3）从小物块放上小车开始，经过t=1．5 s小物块通过的位移大小为多少？