如图所示,光滑的弧形轨道AB和两个粗糙的半圆轨道组成翘尾巴的S形轨道。粗糙的半圆轨道半径为R,两个半圆轨道连接处CD之间留有很小空隙,能够使小球通过,CD之间距离可忽略。光滑弧形轨道最高点A与水平面上B点之间的高度为 =7R。从A点静止释放一个可视为质点的小球,小球沿翘尾巴的S形轨道恰能过最高点E。已知小球质量为m,不计空气阻力,求:
=7R。从A点静止释放一个可视为质点的小球,小球沿翘尾巴的S形轨道恰能过最高点E。已知小球质量为m,不计空气阻力,求:
(1)小球运动到圆弧轨道的B点时对轨道的压力(设此处圆弧半径为R);
(2)小球沿翘尾巴S形轨道运动时克服摩擦力做的功。
随着我国经济和科技的发展,通过引进、创先、研发后,我国具有知识产权的大型运输机已试飞成功,此机可在短时间内投放物资和人员进行救灾、抢险和军事活动,能争取更多时间。现有总质量为 一架大型喷气式飞机,从静止开始滑跑,当位移达到
一架大型喷气式飞机,从静止开始滑跑,当位移达到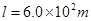 时,速度达到起飞速度
时,速度达到起飞速度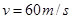 ,在此过程中飞机受到的平均阻力是飞机重力的0.02倍(
,在此过程中飞机受到的平均阻力是飞机重力的0.02倍( 。)求:
。)求:
(1)飞机起飞时的动能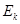 为多大?
为多大?
(2)飞机起飞时的功率P为多大?
(3)若飞机在整个起飞过程中保持功率不变,当速度为30m/s时加速度为多大?
已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。
(1)推导第一宇宙速度v1的表达式;
(2)若卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h,求卫星的运行周期T。
在图中是质量为2.0kg可视为质点的小物块,放在动摩擦因素为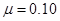 的水桌面上,受到的水平拉力与时间变化的关系如图所示,由静止开始力的作用时间共6秒。完成下列要求(
的水桌面上,受到的水平拉力与时间变化的关系如图所示,由静止开始力的作用时间共6秒。完成下列要求( ):
):

(1)对小物块进行受力分析,并求出滑动摩擦阻力
(2)物体加速运动时的加速度和第1秒末的速度
(3)求出0到6秒物体运动的总位移
2011年8月韩国大邱世界田径锦标赛中的110米栏决赛中,在倒数第二个栏架和最后一个栏架,罗伯斯两次与刘翔发生了碰撞,最后一次还拉拽了刘翔的手,致使刘翔失去平衡,只排在第三位冲过终点,成绩是13秒27,已知110米栏是由110米的跑道和跑道上面的10个跨栏组成的。男子110米栏栏架高度 1.067米,第一栏距起跑线13.72米。栏间距 9.14米,最后一个栏架距终点线的距离 14.02米 。研究人员对刘翔110米栏全过程进行了研究分析,情况比较复杂,在这里,我们把全过程分为三个直线运动阶段,第一个阶段:从起跑到跑到第一个栏时,速度由零增加到全程运动中的最大速度为9.53m/s,近似认为是匀加速运动;第二阶段:一般认为匀速运动,从第一个栏到第十个栏的时间为8.79s,但是由于罗伯斯干扰,跨过第十个栏时的瞬时速度发生突变,第三阶段:最后的冲刺阶段,以跨过第十个栏时的速度开始匀加速运动,直到以全程的最大速度冲过终点,
(1) 求第一阶段所用时间为多少?
(2) 求第三阶段的加速度和跨过第十个栏时的速度为多少?(所有结果都保留三位有效数字)
如图甲所示,空间存在一宽度为2L有界匀强磁场,磁场方向垂直纸面向里。在光滑绝缘水平面内有一边长为L的正方形金属线框,其质量m=1kg、电阻R=4Ω,在水平向左的外力F作用下,以初速度v0=4m/s匀减速进入磁场,线框平面与磁场垂直,外力F大小随时间t变化的图线如图乙所示。以线框右边刚进入磁场时开始计时,求:
(1)匀强磁场的磁感应强度B;
(2)线框进入磁场的过程中,通过线框的电荷量q;
(3)判断线框能否从右侧离开磁场?说明理由。