宜昌市是全国11个重要旅游城市之一,促使了当地的宾馆生意火爆。当地某居民有楼房一幢,室内面积共180 ,拟分隔成两类房间作为旅游客房,大房间每间面积为18
,拟分隔成两类房间作为旅游客房,大房间每间面积为18 ,可住游客5名,每名游客每天住宿费为40元,小房间每间面积为15
,可住游客5名,每名游客每天住宿费为40元,小房间每间面积为15 ,可住游客3名,每名游客每天住宿费为50元,装修大房间每间需要1000元,装修小房间每间需要600元,如果他们只能筹8000元用于装修,且游客能住满客房,它应隔出大房间和小房间各多少间,能获最大利益?
,可住游客3名,每名游客每天住宿费为50元,装修大房间每间需要1000元,装修小房间每间需要600元,如果他们只能筹8000元用于装修,且游客能住满客房,它应隔出大房间和小房间各多少间,能获最大利益?
(本小题14分)请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱(底面是正方形的直棱柱)形状的包装盒,E、F在AB上是被切去的等腰直角三角形HEF斜边的两个端点,设AE=FB=xcm.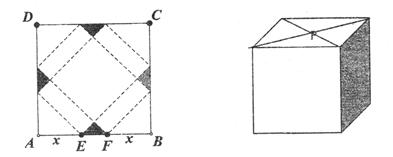
(1)请用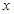 分别表示|GE|、|EH|的长
分别表示|GE|、|EH|的长
(2)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?
|
(3)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
(本小题14分)设函数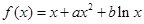 ,曲线
,曲线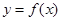 过P(1,0),且在P点处的切斜线率为2.
过P(1,0),且在P点处的切斜线率为2.
(I)求a,b的值;
(II)证明: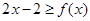 .
.
(本小题14分)如图,四棱锥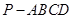 中,底面ABCD为平行四边形,
中,底面ABCD为平行四边形, ,
,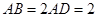 ,
,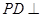 底面ABCD.
底面ABCD.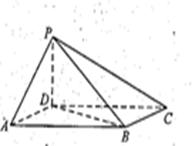
(1)求|DB|的长
(2)证明: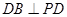 ;
;
(3)若PD=AD,求二面角D-PA-B的余弦值.
(本小题12分)已知函数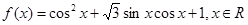 .
.
(1)求函数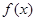 的最小正周期及单调增区间;
的最小正周期及单调增区间;
(2)求函数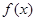 在
在 上的最大值和最小值,并求函数取得最大值和最小值时的自变量
上的最大值和最小值,并求函数取得最大值和最小值时的自变量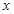 的值.
的值.
已知函数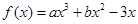 在
在 处取得极值.
处取得极值.
(1)讨论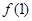 和
和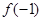 是函数
是函数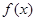 的极大值还是极小值;
的极大值还是极小值;
(2)过点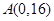 作曲线
作曲线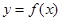 的切线,求此切线方程.
的切线,求此切线方程.