如图所示，在直角△ABC中，∠B=90°，BC=
，∠C=30°，点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是t秒（t>0），过点D作DF⊥BC于点F，连接DE，EF．
（1）求证AE=DF．
（2）四边形AEFD能够成为菱形吗?如果能，求出相应的t的值；如果不能，说明理由．
（3）当t为何值时，△DEF为直角三角形，∠EDF=90°?请说明理由．
已知，一次函数y=x+1的图象与反比例函数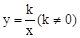
的图象都经过点A（a，2）．
（1）求a的值及反比例函数的表达式；
（2）判断点B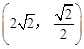
是否在该反比例函数的图象上，请说明理由．
“安全教育，警钟长鸣”，为此，某校随机抽取了九年级（1）班的学生对安全知识的了解情况进行了一次调查统计．图①和图②是通过数据收集后，绘制的两幅不完整的统计图．请你根据图中提供的信息，解答以下问题：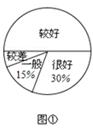
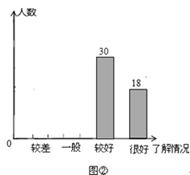
（1）九年级（1）班共有 名学生；
（2）在扇形统计图中，对安全知识的了解情况为“较差”部分所对应的圆心角的度数是 ；
（3）若全校有1500名学生，估计对安全知识的了解情况为“较差”、“一般”的学生共有 名．
如图，在平面直角坐标系中，A（﹣2，2），B（﹣3，﹣2）
（1）若点C与点A关于原点O对称，则点C的坐标为 ；
（2）将点A向右平移5个单位得到点D，则点D的坐标为 ；
（3）由点A，B，C，D组成的四边形ABCD内（不包括边界）任取一个横、纵坐标均为整数的点，求所取的点横、纵坐标之和恰好为零的概率．
解方程组
．
如图，已知直线y=3x﹣3分别交x轴、y轴于A、B两点，抛物线y=x2+bx+c经过A、B两点，点C是抛物线与x轴的另一个交点（与A点不重合）．
（1）求抛物线的解析式；
（2）求△ABC的面积；
（3）在抛物线的对称轴上，是否存在点M，使△ABM为等腰三角形？若不存在，请说明理由；若存在，求出点M的坐标．