阅读下面的材料: 某数学学习小组遇到这样一个问题:如果α,β都为锐角,且 ,
, ,求α+β的度数.该数学课外小组最后是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC.
,求α+β的度数.该数学课外小组最后是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC.

(1)观察图象可知: =∠ABC = °;
=∠ABC = °;
|
(2)请参考该数学小组的方法解决问题:如果 ,
, 都为锐角,当
都为锐角,当 ,
, 时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=
时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=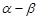 ,并求∠MON的度数.
,并求∠MON的度数.
如图,已知正方形ABCD的边长为4,E是射线CB上的一个动点,过点D作DF⊥DE,交BA的延长线于点F,EF交对角线AC所在的直线于点M,DE交AC于点N .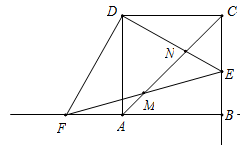
(1)求证:CE=AF;
(2)设CE=x,△AMF的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;
(3)随着点E在射线CB上运动,NA·MC的值是否会发生变化?若不变,请求出NA·MC的值;若变化,请说明理由.
已知抛物线L1: 和抛物线L2:
和抛物线L2: ,其中
,其中 ,抛物线L2与x轴相交于A、B两点,其图像如图所示.
,抛物线L2与x轴相交于A、B两点,其图像如图所示.
(1)下列说法你认为正确的序号是;
①抛物线L1和L2与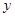 轴交于同一点F
轴交于同一点F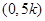 ;② 抛物线L1和L2开口都向上;
;② 抛物线L1和L2开口都向上;
③抛物线L1和L2的对称轴是同一条直线;④ A (-5,0), B(-1,0)
(2)抛物线L1和L2相交于点E、F,当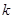 的值发生变化时,请判断线段EF的长度是否发生变化,并说明理由;
的值发生变化时,请判断线段EF的长度是否发生变化,并说明理由;
(3)在(2)中,若抛物线L1的顶点为M,抛物线L2的顶点为N. 问是否存在实数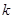 ,使MN=2EF,如存在,求出实数
,使MN=2EF,如存在,求出实数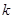 ,如不存在,请说明理由.
,如不存在,请说明理由.
如图2,边长为2的等边△ABC内接于⊙O,△ABC绕圆心O顺时针方向旋转得到△ ,A′C′分别与AB、AC交于E、D点,设旋转角度为
,A′C′分别与AB、AC交于E、D点,设旋转角度为 .
.
(1)当 =,△A′B′C′与△ABC出现旋转过程中的第一次完全重合;
=,△A′B′C′与△ABC出现旋转过程中的第一次完全重合;
(2)当 =60°时(如图1),该图( )
=60°时(如图1),该图( )
A.是中心对称图形但不是轴对称图形
B.是轴对称图形但不是中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形也不是中心对称图形
(3)如图2,当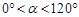 ,△ADE的周长是否会发生变化,如会变化,说明理由,如不会变化,求出它的周长.
,△ADE的周长是否会发生变化,如会变化,说明理由,如不会变化,求出它的周长.
某体育用品商店为了解8月份的销售情况,对本月各类商品的销售情况进行调查,并将调查的结果绘制成如下的两幅不完整的统计图.
(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按8月份球类商品销量的数量购进球类商品,含篮球、足球、排球三种
球,预计恰好用完货款共3600元.设购进篮球x个,足球y个,三种球的进价和售
价如下表:
| 类别 |
篮球 |
足球 |
排球 |
| 进价(单位:元/个) |
50 |
30 |
20 |
| 预售价(单位:元/个) |
70 |
45 |
25 |
求出y与x之间的函数关系式;
(3)在(2)中的进价和售价的条件下,据实际情况,预计足球销售超过60个后,这种
球就会产生滞销,①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)的函数关系式;②求出预估利润的最大值,并写出此时购进三种球各多少个?
如图,将△ABC绕点C旋转180°得到△DEC,过点B作AD的平行线,与ED的延长
线交于点F.
(1)求证:D是EF的中点;
(2)连接BD,当△ABC满足什么条件时,BD⊥EF?并说明其理由.