已知抛物线L1：
和抛物线L2：
，其中
，抛物线L2与x轴相交于A、B两点，其图像如图所示．
（1）下列说法你认为正确的序号是 ；
①抛物线L1和L2与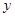
轴交于同一点F
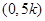； ② 抛物线L1和L2开口都向上；
③抛物线L1和L2的对称轴是同一条直线； ④ A （-5，0）， B（-1，0）
（2）抛物线L1和L2相交于点E、F，当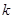
的值发生变化时，请判断线段EF的长度是否发生变化，并说明理由；
（3）在（2）中，若抛物线L1的顶点为M，抛物线L2的顶点为N. 问是否存在实数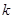，使MN＝2EF，如存在，求出实数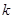，如不存在，请说明理由.
在一副三角板ABC和DEF中，
（1）当AB∥CD，如图①。求∠DCB的度数。
（2）当CD与CB重合时，如图②，判定DE与AC的位置关系，并说明理由。
（3）如图③，当∠DCB等于多少度时，AB∥EC？
列方程解应用题
（1）整理一批图书，如果一个人做要40h完成，现计划由一部分人先做4h，然后增加2人与他们一起做8 h，完成这项工作，假设这些人的工作效率相同，具体应先安排多少人工作？
（2）小颖晚上19点到距家6千米的市少年宫参加“中国梦，我的梦”演讲比赛，比赛开始时间是晚上19点30分。她先以50米/分钟的速度步行走了10分钟，然后乘出租车提前10分钟到达会场，已知小颖所走的市区道路汽车限速为40千米/时，请你计算出租车司机是否超速行驶？（假设出租车为匀速行驶，其它时间忽略不计）
如图，点O为直线CA上一点，∠BOC=45°12′,OD平分∠AOB，∠EOB=90°，求∠AOE和∠DOE的度数。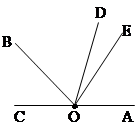
邮购一种图书，每本定价m元，不足100本，另加5%的邮费。
（1）要邮购x本（x小于100），总计金额是多少？
（2）当一次邮购超过100本时，书店除免邮费外，还给予10%的优惠，计算当m=3．2,x=120时，总金额是多少元？
如图：点A、B、C是数轴上三点，其中点C是线段AB的中点，点O表示的是数轴的原点，线段AC比线段OA长1个单位，点B表示的有理数是17，求点C表示的有理数