如图,点O为直线CA上一点,∠BOC=45°12′,OD平分∠AOB,∠EOB=90°,求∠AOE和∠DOE的度数。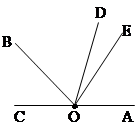
先化简,后求值:

 ,其中
,其中 ,
,
计算: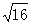 +(
+(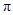
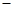 2010)0
2010)0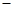
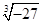 +|
+|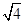
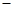 2︱
2︱
因式分解:(1) ;(2)2a2-12a+18
;(2)2a2-12a+18
现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线.
(1)已知∠AOC=30°,∠BOD=60°,求∠MON的度数;
(2)如果只有已知“∠COD=90°”,你能求出∠MON的度数吗?如果能,请求出;如果不能,请说明理由.