如图，抛物线y=
+3与x轴相交于A、B，与直线y=－
x+b相交于B、C，直线y=－x+b与y轴交于点E．
（1）求直线BC的表达式；
（2）求△ABC的面积；
（3）若点M在线段AB上以每秒1个单位长度的速度从A向B运动（不与A、B重合），同时，点N在射线BC上以每秒2个单位长度的速度从B向C运动．设运动时间为t秒，请写出△MNB的面积s与t的函数关系式，并求出点M运动多少时间时，△MNB的面积最大，最大面积是多少？
如图，
信封中装有两张卡片，卡片上分别写着7cm、3cm；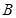
信封中装有三张卡片，卡片上分别写着2cm、4cm、6cm；信封外有一张写着5cm的卡片．所有卡片的形状、大小都完全相同．现随机从两个信封中各取出一张卡片，与信封外的卡片放在一起，用卡片上标明的数量分别作三条线段的长度．用画树状图法，求这三条线段能组成三角形的概率.
已知：如图，Rt△ABC≌Rt△ADE，∠ABC＝∠ADE=90°，试以图中标有字母的点为端点，连结两条线段，如果你所连结的两条线段满足相等、垂直或平行关系中的一种，那么请你把它写出来并证明．
已知一元二次方程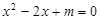
。
（1）若方程有两个不相等实数根，求m的范围；
（2）若方程的两个相等的实数根，求m的值。
画出图中三棱柱的三视图。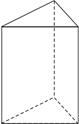
解方程
①
②(x-3)2="2(3-x)"