如图，在平面直角坐标系中，二次函数y=﹣
+bx的图像经过点A（4，0）．点E是过点C（2,0）且与y轴平行的直线上的一个动点，过线段CE的中点G作DF⊥CE交二次函数的图像于D、F两点．
（1）求二次函数的表达式．
（2）当点E落在二次函数的图像的顶点上时，求DF的长．
（3）当四边形CDEF是正方形时，请直接写出点E的坐标．
某公司组织340名员工进行长途考察活动，带有行李170件，计划租用甲、乙两种型号的汽车共10辆，经了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李。（1）请你帮助公司设计三个可行的租车方案；
（2）如果甲车的租金为每辆2000元，乙车的租金为每辆1800元，请你设计租车费用最省的方案？
如图等腰三角形ABC中，AB=AC=3，BC=2
（1）求作一个圆，使它经过A、B、C三点（保留作图痕迹）；
（2）求所作圆的直径长.
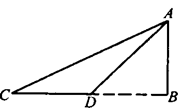
如图，河岸边有座水塔AB，测量人员在河对岸C处测得塔顶A的仰角为300，然后沿着CB方向前进30米到达D处，又测得A的仰角为450，请根据上述数据计算水塔的高(结果精确到0.1)（
）.
．
有一个不透明口袋，装有分别标有数字1，2，3，4的4个小球（小球除数字不同外，其余都相同），另有3张背面完全一样、正面分别写有数字1，2，3的卡片．小敏从口袋中任意摸出一个小球，小颖从这3张背面朝上的卡片中任意摸出一张，然后计算小球和卡片上的两个数的和．请你用列表或画树状图的方法，求摸出的这两个数的和为5的概率.
．
若方程组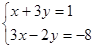
的解所对应的点在一次函数
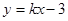的图象上，求
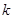的值.