宾哥和君哥在华润广场前感慨楼房真高.君哥说:“这楼起码20层!”宾哥却不以为然:“20层?我看没有,数数就知道了!”君哥说:“老大,你有办法不用数就知道吗?”宾哥想了想说:“没问题!让我们来量一量吧!”君哥、宾哥在楼体两侧各选A、B两点,其中矩形CDEF表示楼体,AB=200米,CD=20米,∠A=30°,∠B=45°,(A、C、D、B四点在同一直线上)问: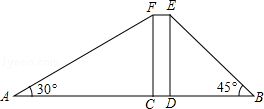
(1)楼高多少米?(用含根号的式子表示)
(2)若每层楼按3米计算,你支持宾哥还是君哥的观点呢?请说明理由.(精确到0.1,参考数据: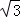 ≈1.73,
≈1.73,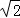 ≈1.41,
≈1.41,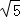 ≈2.24)
≈2.24)
如图1,在正方形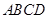 中,点
中,点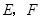 分别为边
分别为边 的中点,
的中点,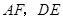 相交于点
相交于点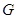 ,则可得结论:①
,则可得结论:①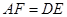 ;②
;②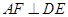 .(不需要证明)
.(不需要证明)
(1)如图2,若点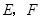 不是正方形
不是正方形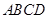 的边
的边 的中点,但满足
的中点,但满足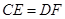 ,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
(2)如图3,若点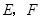 分别在正方形
分别在正方形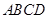 的边
的边 的延长线和
的延长线和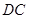 的延长线上,且
的延长线上,且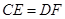 ,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
(3)如图4,在(2)的基础上,连接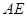 和
和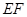 ,若点
,若点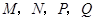 分别为
分别为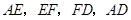 的中点,请判断四边形
的中点,请判断四边形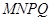 是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
阅读下面材料,再回答问题:
有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”。
解决下列问题:
(1)菱形的“二分线”可以是。
(2)三角形的“二分线”可以是。
(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.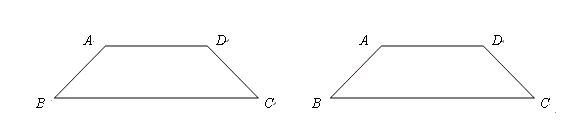
第41届上海世博会于2010年5月1日开幕,它将成为人类文明的一次精彩对话.某小型企业被授权生产吉祥物海宝两种造型玩具,生产每种造型所需材料及所获利润如下表:
该企业现有A种材料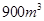 ,B种材料
,B种材料 ,计划用这两种材料生产2000个海宝造型玩具.设该企业生产甲造型玩具
,计划用这两种材料生产2000个海宝造型玩具.设该企业生产甲造型玩具 个,生产这两种造型的玩具所获利润为
个,生产这两种造型的玩具所获利润为 元.(1)求出
元.(1)求出 应满足的条件,并且说出有多少种符合题意的生产方案?(2)写出
应满足的条件,并且说出有多少种符合题意的生产方案?(2)写出 与
与 的关系式.(3)请你给该企业推荐一种生产方案,并说明理由.
的关系式.(3)请你给该企业推荐一种生产方案,并说明理由.
甲、乙两支篮球队在集训期内进行了五场比赛,将比赛成绩进行统计后,绘制成如图1、图2的统计图.(1)已知甲队五场比赛成绩的平均分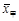 =90分,请你计算乙队五场比赛成绩的平均分
=90分,请你计算乙队五场比赛成绩的平均分 ;(2)就这五场比赛,分别计算两队成绩的极差;(3)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计情况,试从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
;(2)就这五场比赛,分别计算两队成绩的极差;(3)如果从甲、乙两队中选派一支球队参加篮球锦标赛,根据上述统计情况,试从平均分、折线的走势、获胜场数和极差四个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?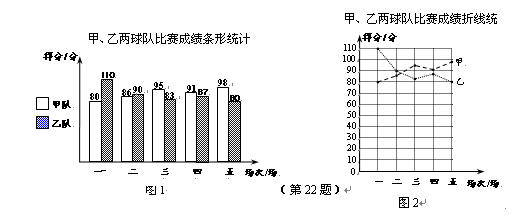
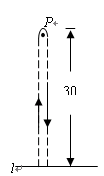
甲、乙两同学玩“托球赛跑”游戏,商定:用球拍托着乒乓球从起跑线l起跑,绕过P点跑回到起跑线(如图所示);途中乒乓球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲同学由于心急,掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,甲同学说:“我俩所用的全部时间的和为50秒”,乙同学说:“捡球过程不算在内时,甲的速度是我的1.2倍”.根据信息,问哪位同学获胜?(转身拐弯处路程可忽略不计)