如图①所示的晾衣架，支架的基本图形是菱形，其示意图如图②，晾衣架伸缩时，点G在射线DP上滑动，∠CED的大小也随之发生变化，已知每个菱形边长均为20cm，且AH＝DE＝EG＝20cm．
(1)当∠CED＝60°时，求C，D两点间的距离．
(2)当∠CED由60°变为120°时，点A向左移动了多少厘米？(结果精确到0.1cm)
(3)设DG＝xcm，当∠CED的变化范围为60°～120°(包括端点值)时，求x的取值范围．(结果精确到0.1cm)
(参考数据：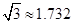
，可使用科学计算器)
有一张明星演唱会的门票，小明和小亮都想获得这张门票，亲自体验明星演唱会的热烈气氛，小红为他们出了一个主意，方法就是：从印有1、2、3、4、5、4、6、7的8张扑克牌中任取一张，抽到比4大的牌，小明去；否则，小亮去．求小明抽到4的概率
你认为这种方法对小明和小亮公平吗？请说明理由；若不公平，请你修改游戏规则，使游戏对双方都公平．
已知：如图，AD⊥BC，EF⊥BC，∠1=∠2．求证：AB∥GF．
推理填空 每空１分
如图，已知：∠BDG＋∠EFG＝180°，∠DEF＝∠B.试判断∠AED与∠C的大小关系，并加以说明
如图所示，A、B是4×5网格中的格点（网格线的交点），网格中的每个小正方形的边长都是1．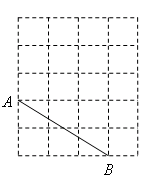
请在图中标出使以A、B、Ｃ为顶点的三角形是等腰三角形的所有格点Ｃ的位置（分别用
依次标出）．若以点A为坐标原点建立平面直角坐标系，求直线BC的解析式．（只需求一条即可）
为丰富同学们的课余生活，学校将组织一次外出旅游活动，甲乙两家旅行社都提出优惠条件，甲旅行社表示每人都打八折，乙旅行社表示领队的20名教师免费，学生一律打九折，两家旅行社的报价都是每人300元。请你写出两家旅行社所收总旅行费y（元）与学生人数x之间的函数关系。
为节省费用，你将选择哪家旅行社，请说出理由