如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30%,求雕塑的高度CD.(最后结果精确到0.1米,参考数据: )
)
如图,平行四边形 ABCD对角线交于点O,点E是线段BO上的动点(与点B、O不重合),连接CE,过A点作AF∥CE交BD于点F,连接AE与CF.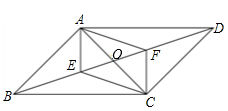
(1)求证:四边形AECF是平行四边形;
(2)当BA=BC=2,∠ABC=60°时,平行四边形 AECF能否成为正方形?若能,求出BE的长;若不能,请说明理由.
某校九年级(1)班所有学生参加2014年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题: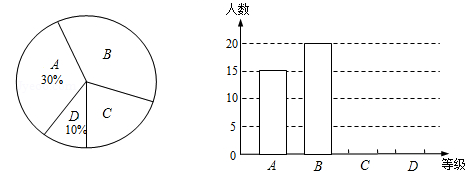
(1)九年级(1)班参加体育测试的学生有_________人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是___,等级C对应的圆心角的度数为___°;
(4)若该校九年级学生共有850人参加体育测试,请估计达到A级和B级的学生共有多少人?
如图,直线 的解析表达式为
的解析表达式为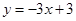 ,且
,且 与
与 轴交于点D,直线
轴交于点D,直线 经过点A,B,直线
经过点A,B,直线 和
和 交于点C.
交于点C.
(1)求直线 的解析表达式;
的解析表达式;
(2)求△ADC的面积;
(3)直线 上存在异于点C的另一点P,使△ADP与△ADC面积相等,求出点P的坐标.
上存在异于点C的另一点P,使△ADP与△ADC面积相等,求出点P的坐标.
如图,已知四边形ABCD是平行四边形,若点E、F分别在边BC、AD上,连接AE、CF,请再从下列三个备选条件中,选择添加一个恰当的条件.使四边形AECF是平行四边形,并予以证明.
备选条件:AE=CF,BE=DF,∠AEB=∠CFD,
我选择添加的条件是.
证明:
已知,若函数 是关于x的一次函数.
是关于x的一次函数.
(1)求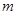 的值,并写出解析式;
的值,并写出解析式;
(2)判断点(1,2)是否在此函数图像上,说明理由.